chaos theory
chaos theory
카오스 이론이 진짜 무엇인가: 비선형 결정론적 시스템에 대한 깊은 잠수
카오스 이론은 20세기와 21세기의 가장 심오하고 오해받는 과학적 틀 중 하나이다. 사실 그것은 '무질서'나 '무작위'에 관한 것이라기보다는 결정론적 시스템이 어떻게 예측할 수 없는 행동을 나타낼 수 있는지에 대한 수학적 연구이다. 이 게시물에서 우리는 카오스 이론의 기원, 수학, 정의적 특성 및 실제 응용을 탐구한다. 목적은 근거 있고 엄격한 개요를 제시하여 용어를 은유나 감정이 아니라 구조와 진실을 통해 이해하는 것이다.
---
I. 기원과 역사발전
카오스 이론은 수학, 기상학, 비선형 역학의 융합에서 공식적으로 등장했다. 19세기에 앙리 푸앵카레의 삼체 문제 연구를 통해 초기 힌트가 나타났지만, 현대 분야에 불을 지핀 것으로 평가받는 사람은 1960년대 기상학자 에드워드 로렌츠였다. 그의 수치 시뮬레이션은 초기 조건의 극소한 차이가 기상 모델에서 극적으로 다른 결과를 초래할 수 있음을 보여주었는데, 이 현상을 나중에 그는 "나비 효과"라고 불렀다.
결정론적 혼돈이라는 표현은 정확한 규칙(결정론적 방정식)을 따르지만 진화가 초기 조건에 너무 민감하여 장기 예측이 불가능해지는 시스템을 반영하기 위해 만들어졌다. 이것은 무작위성이 아니라 질서와 무질서의 경계에 있는 역동적인 춤인 구조화된 예측 불가능성이었다.
---
II. 카오스의 수학적 기초
카오스 이론은 단지 철학적인 것이 아니라 수학적인 것이다. 그 기초는 비선형 미분 방정식, 이산 시간 지도 및 동적 시스템에 있다. 핵심 기능에는 다음이 포함됩니다.
초기 조건에 대한 민감도: 종종 랴푸노프 지수를 통해 공식화되며, 이는 위상 공간에서 근처 궤적의 기하급수적 발산을 나타낸다. 시작 값의 작은 차이는 결과의 기하급수적으로 증가하는 차이로 이어진다.
위상 혼합: 시스템은 복잡한 상호 연결성을 반영하여 위상 공간의 모든 영역이 결국 다른 영역과 겹치는 방식으로 진화한다.
밀도가 높은 주기 궤도: 혼돈계 내에는 이상한 끌개 내에 조밀하게 채워진 무한한 주기 궤도 세트가 존재하며, 이는 혼돈이 구조의 부재가 아니라 예측 불가능성 내에 무한한 구조를 내장하는 것임을 보여준다.
프랙탈과 이상한 끌개: 많은 혼돈 시스템은 로렌츠 끌개 또는 뢰슬러 끌개와 같은 정수가 아닌 차원 끌개를 향해 진화한다. 이들은 자기 유사성과 비유클리드 기하학을 나타내며 규모에 걸쳐 복잡한 재귀적 거동을 나타낸다.
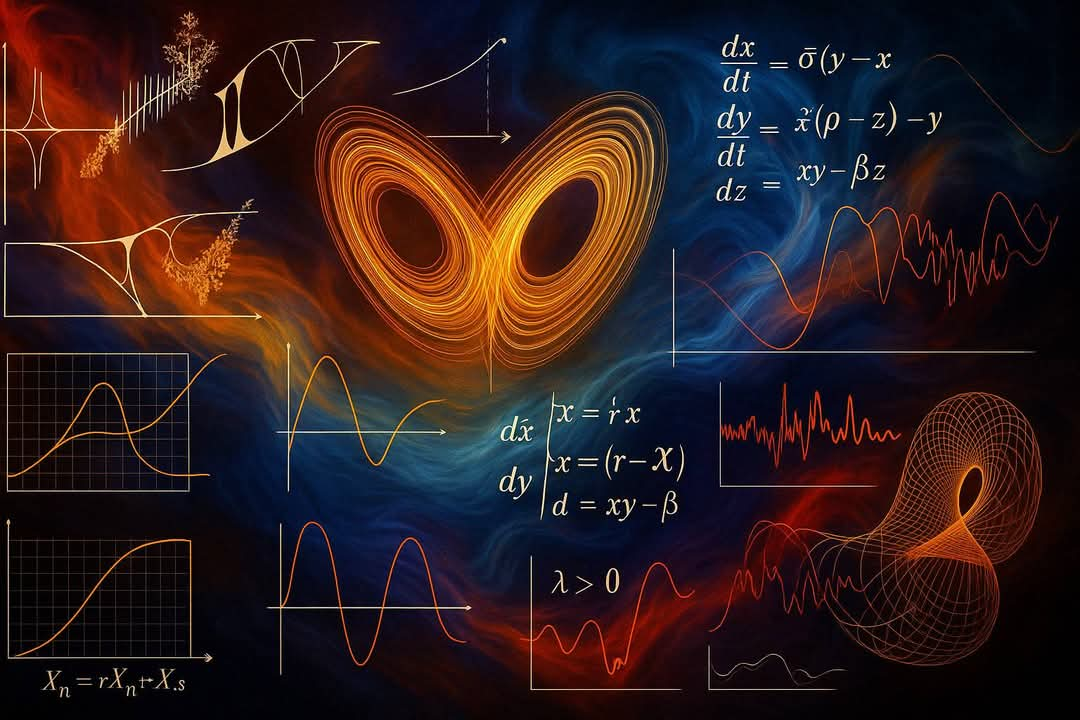
III. 핵심 방정식과 예
로렌츠 시스템(1963):
세 개의 결합된 미분 방정식의 시스템:
dx/dt = σ(y - x)
dy/dt = x(ρ - z) - y
dz/dt = xy - βz
이 방정식들은 대기 대류를 모델링하며, 그 해들은 유명한 나비 모양의 끌개를 형성합니다.
로지스틱 맵:
xₙ₊₁ = r * xₙ * (1 - xₙ)
매개변수 r에 따라 고정점, 분기점 및 완전한 혼돈을 나타내는 기만적으로 간단한 방정식이다.
--
IV. 카오스 이론의 응용
카오스 이론은 이론에 국한되지 않습니다. 다양한 분야에 걸친 실용적인 통찰력을 뒷받침합니다.
기상학: 기상 시스템은 고전적인 혼돈 시스템입니다. 예측성은 초기 조건에 대한 민감성으로 인해 시간이 지남에 따라 저하된다.
생태학: 포식자-피식자 역학과 개체군 주기는 비선형 피드백 조건에서 혼돈스러운 행동을 나타낸다.
엔지니어링: 진동 분석, 회로 설계 및 유체 역학은 시스템 안정성을 보장하기 위해 혼돈 모델링이 필요합니다.
신경과학: 뇌파 패턴과 특정 간질 발작은 전기 활동에서 혼돈의 특징을 보여준다.
경제 및 시장: 논란의 여지가 있지만 변동성과 티핑 포인트를 이해하기 위해 혼돈 기반 모델을 통해 비선형 금융 시스템이 연구되었습니다.

V. 오해와 오용
혼돈 이론은 “모든 것이 무작위적”이거나 “파괴는 본질적으로 창조적”이라고 제안하지 않는다. 복잡성이 존재한다는 것이 자동적으로 어떤 것이 혼란스럽다는 것을 의미하는 것도 아닙니다. 위의 기준을 충족하는 특정 부류의 결정론적 체계에만 적용된다. 카오스 이론에서 끌어낸 많은 은유들은 시적이지만, 기술적으로는 옳지 않다. 은유와 수학 사이의 경계가 어디에 있는지 이해하는 것은 과학적 정확성을 보존하는 데 중요합니다.

VI. 왜 중요한가
혼돈 이론은 법칙에 의해 지배되는 우주에서도 예측 가능성은 제한적이라는 것을 밝힌다. 모델링에서 겸손함, 계산에서 정밀함, 가정에서 신중함을 가르쳐줍니다. 더 깊은 수준에서는 질서와 복잡성 사이의 다리를 제공하여 가장 작은 입력이 전체 시스템에 어떻게 반향을 일으킬 수 있는지 보여줍니다. 구어체의 혼돈에 관한 것이 아니라 숨겨진 질서의 수학에 관한 것이다.
---
클로징:
카오스 이론은 미학적이지 않습니다. 은유가 아닙니다. 그것은 슬로건이 아닙니다. 그것은 수십 년에 걸쳐 실제 응용, 형식 수학, 그리고 아름다운 깊이로 구축된 학문입니다. 우리의 책임은 그것을 그렇게 이해하는 것이다. 그것을 개발한 사람들의 일을 존중하고, 그것이 요구하는 도구인 수학, 이성, 구조화된 탐구를 사용하여 그것과 참여하는 것이다.

#카오스이론 #비선형역학 #결정론적카오스 #로렌츠어트랙터 #프랙탈지오메트리 #랴푸노프지수 #복잡시스템즈 #과학문학 #시스템즈 사고 #수학 #과학적 진실 #인식론 #카오스틱시스템즈
What Chaos Theory Really Is: A Deep Dive into Nonlinear Deterministic Systems
---
Chaos Theory is one of the most profound and misunderstood scientific frameworks of the 20th and 21st centuries. Far from being about “disorder” or “randomness,” it is, in fact, a mathematical study of how deterministic systems can exhibit unpredictable behavior. In this post, we explore the origin, the mathematics, the defining characteristics, and the real-world applications of Chaos Theory. The aim is to present a grounded and rigorous overview, so that the term is understood not through metaphor or emotion—but through structure and truth.
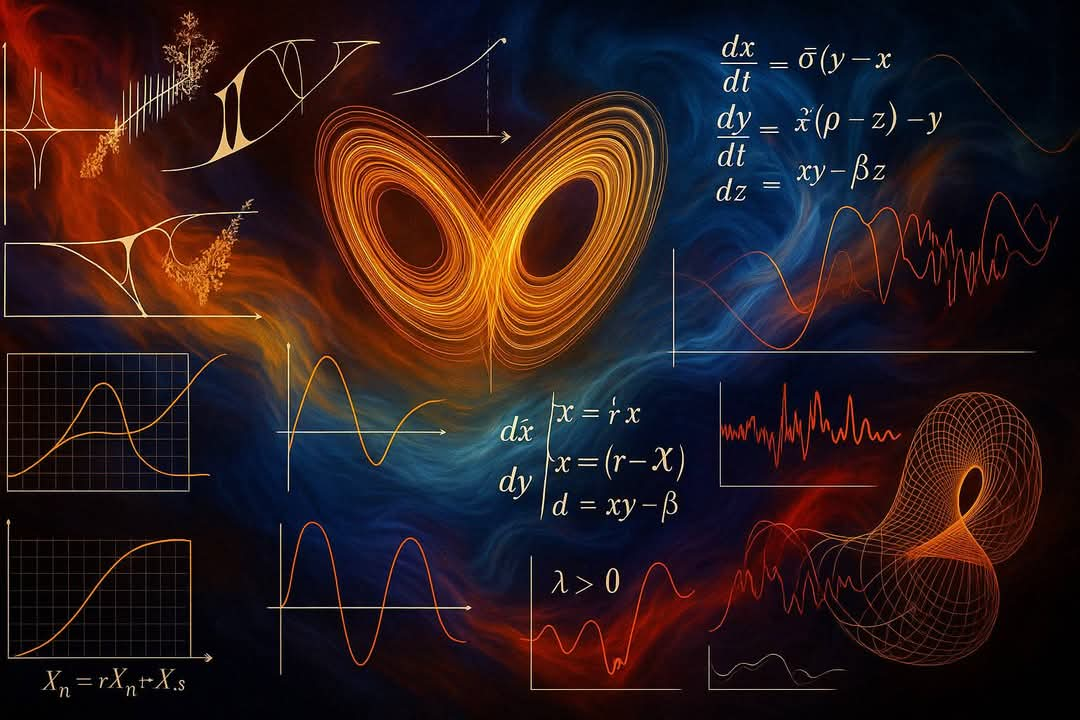
I. Origins and Historical Development
Chaos Theory formally emerged from a convergence of mathematics, meteorology, and nonlinear dynamics. Although early hints appeared in the 19th century through the work of Henri Poincaré on the three-body problem, it was Edward Lorenz, a meteorologist in the 1960s, who is credited with igniting the modern field. His numerical simulations revealed that infinitesimally small differences in initial conditions could lead to dramatically different outcomes in a weather model—a phenomenon he later termed the “butterfly effect.”
The phrase deterministic chaos was coined to reflect systems that obey precise rules (deterministic equations), yet whose evolution is so sensitive to initial conditions that long-term prediction becomes impossible. This was not randomness, but rather structured unpredictability—a dynamic dance on the edge of order and disorder.
-

II. Mathematical Foundations of Chaos
Chaos Theory is not just philosophical—it is mathematical. Its foundation lies in nonlinear differential equations, discrete-time maps, and dynamical systems. Core features include:
Sensitivity to Initial Conditions: Often formalized through Lyapunov exponents, this refers to the exponential divergence of nearby trajectories in phase space. Small differences in starting values lead to exponentially growing differences in outcome.
Topological Mixing: The system evolves in such a way that any region of the phase space eventually overlaps with any other, reflecting complex interconnectivity.
Dense Periodic Orbits: Within chaotic systems, there exist infinite sets of periodic orbits that are densely packed within the strange attractor—showing that chaos is not the absence of structure, but the embedding of infinite structure within unpredictability.
Fractals and Strange Attractors: Many chaotic systems evolve toward non-integer dimensional attractors, such as the Lorenz attractor or the Rössler attractor. These exhibit self-similarity and non-Euclidean geometry, revealing complex recursive behavior across scales.

III. Key Equations and Examples
Lorenz System (1963):
A system of three coupled differential equations:
dx/dt = σ(y - x)
dy/dt = x(ρ - z) - y
dz/dt = xy - βz
These equations model atmospheric convection, and their solutions form the famous butterfly-shaped attractor.
Logistic Map:
xₙ₊₁ = r * xₙ * (1 - xₙ)
A deceptively simple equation that, depending on the parameter r, exhibits fixed points, bifurcations, and full-blown chaos.
---
IV. Applications of Chaos Theory
Chaos Theory is not confined to theory—it underpins practical insights across diverse fields:
Meteorology: Weather systems are classic chaotic systems. Predictability degrades over time due to sensitivity to initial conditions.
Ecology: Predator-prey dynamics and population cycles exhibit chaotic behavior under nonlinear feedback conditions.
Engineering: Vibration analysis, circuit design, and fluid dynamics require chaos modeling to ensure system stability.
Neuroscience: Brainwave patterns and certain epileptic seizures show chaotic signatures in electrical activity.
Economics and Markets: While controversial, nonlinear financial systems have been studied through chaos-based models to understand volatility and tipping points.

V. Misconceptions and Misuse
Chaos Theory does not suggest that “everything is random” or that “disruption is inherently creative.” Nor does it imply that the presence of complexity automatically means something is chaotic. It applies only to certain classes of deterministic systems that meet the criteria above. Many metaphors drawn from Chaos Theory are poetic, but not technically correct. Understanding where the boundary lies between metaphor and mathematics is critical for preserving scientific accuracy.
---
VI. Why It Matters
Chaos Theory reveals that even in a universe governed by laws, predictability is limited. It teaches us humility in modeling, precision in computation, and caution in assumptions. At a deeper level, it offers a bridge between order and complexity—showing how the smallest of inputs can reverberate across entire systems. It is not about chaos in the colloquial sense—it is about the mathematics of hidden order.
---
In Closing:
Chaos Theory is not aesthetic. It is not metaphor. It is not a slogan. It is a discipline, built over decades, with real-world applications, formal mathematics, and beautiful depth. Our responsibility is to understand it as such—to respect the work of those who developed it, and to engage with it using the tools it demands: math, reason, and structured inquiry.
---
#ChaosTheory #NonlinearDynamics #DeterministicChaos #LorenzAttractor #FractalGeometry #LyapunovExponent #ComplexSystems #ScienceLiteracy #SystemsThinking #Mathematics #ScientificTruth #Epistemology #ChaoticSystems