수소 원자의 바닥 상태(1s 오비탈)에 대한 시간에 따른 파동 함수
Wave function over time for the ground state (1s orbital) of hydrogen atoms

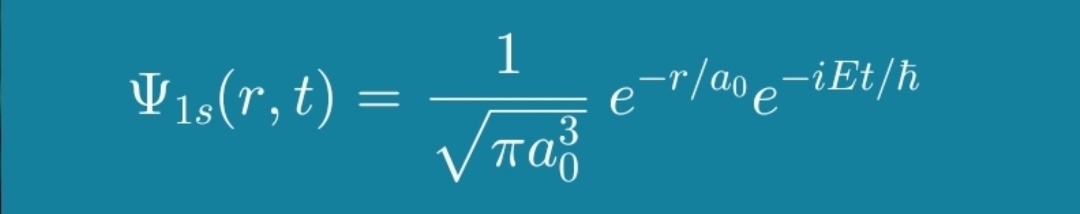
이 식은 수소 원자의 바닥 상태(1s 오비탈)에 대한 시간에 따른 파동 함수를 나타냅니다. 각 부분을 자세히 살펴보겠습니다.
- Ψ₁ₛ(r, t): 이것은 수소 원자의 전자 파동 함수를 나타냅니다. Ψ(Psi)는 파동 함수의 기호이며, 아래 첨자 "1s"는 바닥 상태(주양자수 n=1, 방위 양자수 l=0)를 나타내고, 'r'은 원자핵으로부터의 반지름 거리를, 't'는 시간을 나타냅니다. 파동 함수는 특정 위치와 시간에 전자를 발견할 확률 진폭을 설명합니다.
- 1 / √(πa₀³): 이것은 정규화 상수입니다. 이것은 전자를 공간의 어딘가에서 발견할 확률이 1이 되도록 합니다. a₀ 는 보어 반지름으로, 수소 원자에서 전자와 양성자 사이의 가장 가능성이 높은 거리를 나타내는 기본 상수입니다.
- e⁻ʳ/ₐ₀: 이것은 파동 함수의 반지름 부분입니다. 이것은 전자를 발견할 확률이 원자핵으로부터의 거리(r)에 따라 어떻게 달라지는지 설명합니다. 지수 항은 원자핵으로부터의 거리가 증가함에 따라 확률이 지수적으로 감소함을 나타냅니다.
- e⁻ⁱᴱᵗ/ħ: 이것은 파동 함수의 시간 의존 부분입니다. 이것은 파동 함수가 시간에 따라 어떻게 변하는지 설명합니다. 'i'는 허수 단위(√-1)이고, 'E'는 1s 오비탈에서 전자의 에너지(음수 값으로, 속박 상태를 나타냄), 't'는 시간이고, 'ħ'(h-bar)는 환산 플랑크 상수(h/2π)입니다. 이 항은 시간에 따라 진동하는 위상 인자를 도입합니다.
요약하자면: 이 식은 수소 원자의 바닥 상태에서 전자의 거동을 공간 분포와 시간적 진화를 모두 포함하여 완벽하게 수학적으로 설명합니다. 이 파동 함수로부터 확률 밀도(|Ψ₁ₛ(r, t)|²)를 계산하여 특정 시간에 특정 위치에서 전자를 발견할 가능성을 결정할 수 있습니다.

This equation represents the wave function over time for the ground state (1s orbital) of the hydrogen atom. Let's take a closer look at each part.
- Ψ1s(r, t): This represents the electron wave function of the hydrogen atom. Ψ(Psi) is the symbol of the wave function, and the subscript "1s" represents the ground state (main quantum number n=1, azimuth quantum number l=0), 'r' represents the radial distance from the nucleus, and 't' represents time. The wave function describes the probability amplitude of discovering electrons at a specific location and time.
- 1 / √(πa03): This is a normalization constant. This makes the probability of finding electrons somewhere in space 1. a0 is the Bohr radius, which is the fundamental constant that represents the most likely distance between electrons and protons in a hydrogen atom.
- e−r/a0: This is the radial part of the wave function. This explains how the probability of discovering an electron depends on the distance (r) from the nucleus. An exponential term indicates that the probability decreases exponentially as the distance from the nucleus increases.
- e−iEt/ħ: This is the time dependent part of the wave function. This explains how the wave function changes over time. 'i' is an imaginary unit (√-1), 'E' is the energy of electrons in the 1s orbital (negative values, indicating the bound state), 't' is time, and 'ħ' (h-bar) is the converted Planck constant (h/2π). This term introduces a phase factor that oscillates with time.
To summarize: This equation describes the behavior of electrons in the ground state of hydrogen atoms perfectly mathematically, including both spatial distribution and temporal evolution. From this wave function, the probability density (|Ψ1s(r, t)|2) can be calculated to determine the likelihood of finding electrons at a particular location at a particular time.
참고 : Quantum number

이 이미지는 양자수(Quantum Numbers)에 대한 설명입니다. 이것은 연구 논문이 아니고 교육 자료입니다. 주요 내용은 다음과 같습니다.
- 양자수의 개념: 전자의 위치와 에너지를 설명하는 네 가지 양자수 (주양자수, 방위양자수, 자기양자수, 스핀양자수)를 소개합니다.
- 각 양자수의 의미:
- 주양자수 (Principal Quantum Number, n): 전자 껍질(shell)의 에너지 준위와 크기를 나타냅니다. n=1, 2, 3... 등의 값을 가집니다.
- 방위양자수 (Azimuthal Quantum Number, l): 부껍질(subshell)의 모양을 나타냅니다. l = 0 (s), 1 (p), 2 (d), 3 (f) 등의 값을 가지며, n-1까지의 값을 가집니다.
- 자기양자수 (Magnetic Quantum Number, m): 공간에서 궤도의 방향을 나타냅니다. -l부터 +l까지의 값을 가집니다.
- 스핀 양자수 (Spin Quantum Number, s): 전자의 스핀을 나타냅니다. +1/2 또는 -1/2의 값을 가집니다.
- 파울리 배타 원리: 같은 궤도에 있는 두 개의 전자는 같은 스핀을 가질 수 없다는 것을 설명합니다.
- 각 껍질의 최대 전자 수: 각 껍질이 가질 수 있는 최대 전자 수 (2n²)를 설명합니다.
요약하자면, 이 이미지는 화학이나 물리학 교육 자료로, 특정 연구 논문의 내용이 아닙니다.
More detail. ..