특수정적분문제와 해
A lot of special definite integral problems
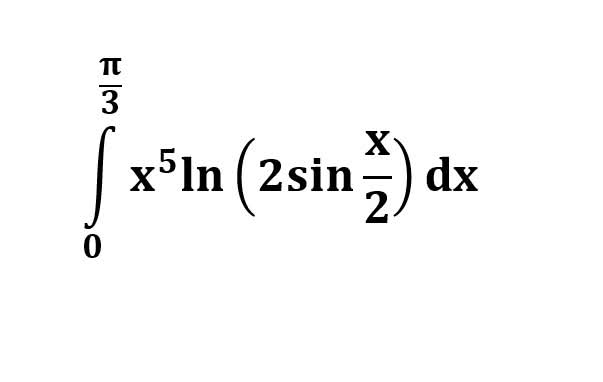
주어진 정적분은 다음과 같습니다.

이 정적분은 기본적인 함수를 사용하여 해석적으로 풀 수 없습니다. 근삿값을 구하기 위해 수치적 방법을 사용해야 합니다. 간단한 대수적 조작이나 표준 적분 기법으로는 이 문제를 직접적으로 풀 수 없습니다.
이 문제가 어려운 이유와 근삿값을 구하는 방법을 살펴보겠습니다.
이 적분이 어려운 이유
1. 함수의 곱: 피적분 함수는 x^5와 \ln(2\sin(\frac{x}{2}))의 곱입니다. 곱의 적분을 위한 간단한 공식은 없습니다. 부분적분이 떠오를 수 있지만, 점점 더 복잡한 적분으로 이어질 것입니다.
2. 로그 함수: 자연로그는 추가적인 복잡성을 가져옵니다. \ln(x)의 적분에 대한 규칙이 있지만, 여기서의 인수는 2\sin(\frac{x}{2})이므로 이러한 규칙을 직접 적용할 수 없습니다.
3. 삼각함수: 로그 안의 사인 함수는 또 다른 어려움을 더합니다. 일부 삼각함수는 직접 적분할 수 있지만, 로그와의 조합은 적분을 불가능하게 만듭니다.
수치적 근사 방법
근삿값을 구하려면 수치적 적분 기법을 사용해야 합니다. 두 가지 일반적인 방법은 다음과 같습니다.
1. 사다리꼴 공식: 이 방법은 곡선 아래의 면적을 사다리꼴로 나누어 적분을 근사합니다. 공식은 다음과 같습니다

여기서 n은 사다리꼴의 개수이고, x_i = a + i\frac{b-a}{n}입니다.
2. 심슨 공식: 이 방법은 포물선을 사용하여 곡선을 근사하므로 일반적으로 사다리꼴 공식보다 정확도가 높습니다.
공식은 다음과 같습니다.

여기서 n은 짝수여야 합니다.
두 방법 모두 구간 [0, \frac{\pi}{3}] 내의 여러 지점에서 피적분 함수를 계산해야 합니다. 이것은 소프트웨어나 계산기를 사용하여 수행할 수 있습니다.
수치적 적분을 위한 소프트웨어 사용
Mathematica, MATLAB, Python의 SciPy 라이브러리 또는 Wolfram Alpha와 같은 소프트웨어는 정적분의 수치적 근사값을 직접 계산할 수 있습니다. 이러한 도구는 대부분의 경우 수동으로 사다리꼴 또는 심슨 공식을 적용하는 것보다 정확하고 효율적인 정교한 알고리즘을 사용합니다. 단순히 적분을 입력하면 소프트웨어가 근삿값을 제공합니다.
Python의 SciPy를 사용한 예:
import numpy as np
from scipy.integrate import quad
def integrand(x):
return x**5 * np.log(2*np.sin(x/2))
result, error = quad(integrand, 0, np.pi/3)
print(f"근삿값: {result}")
print(f"추정 오차: {error}")
이 코드는 적분의 근삿값과 오차의 추정치를 출력합니다.
답변
적분의 복잡성으로 인해 정확한 해석적 해는 구할 수 없습니다. 근삿값을 얻으려면 수치적 방법이 필요합니다. 계산 도구를 사용하는 것이 가장 효과적인 방법입니다. 위의 Python 코드는 이를 수행하는 방법을 제공합니다. 구체적인 수치 값은 사용된 수치적 적분 방법의 정밀도에 따라 달라집니다.
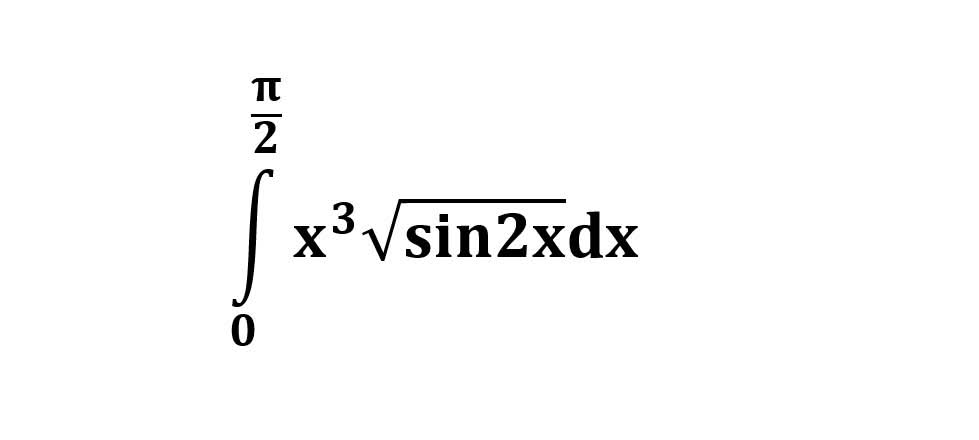
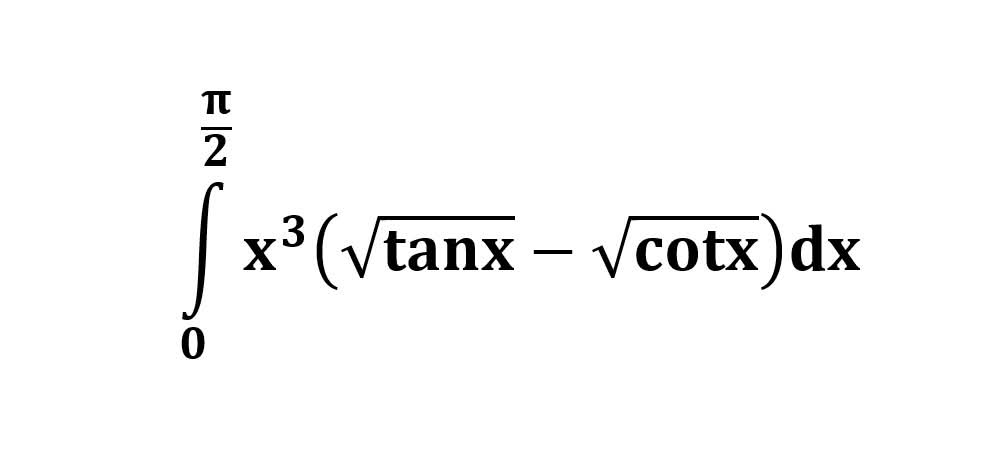
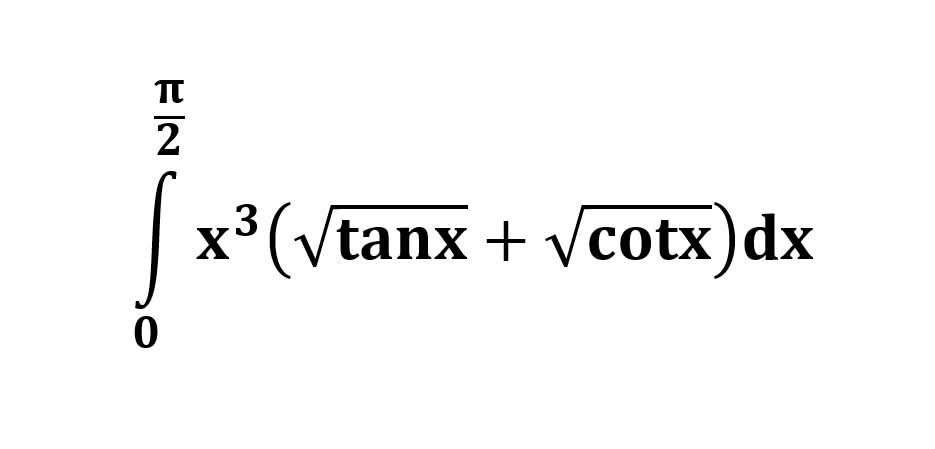
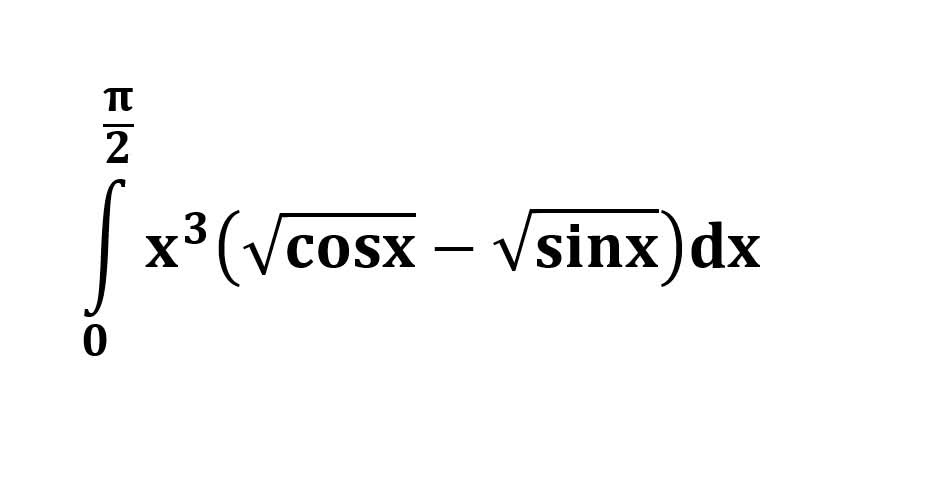
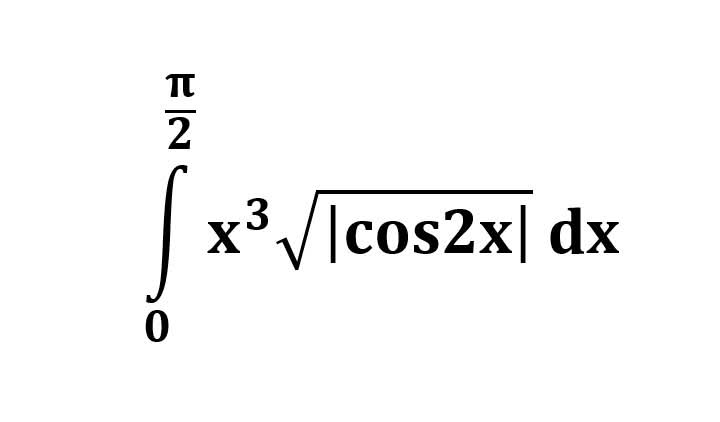
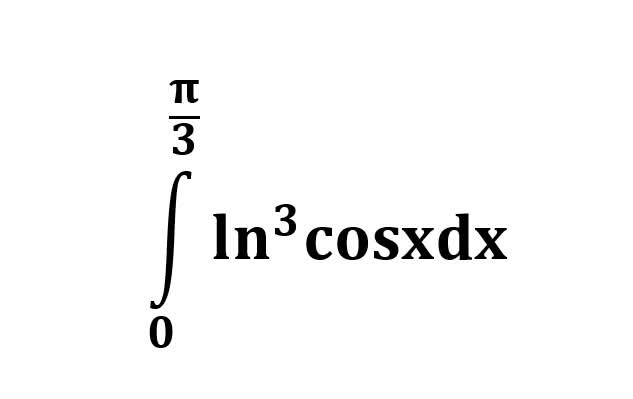
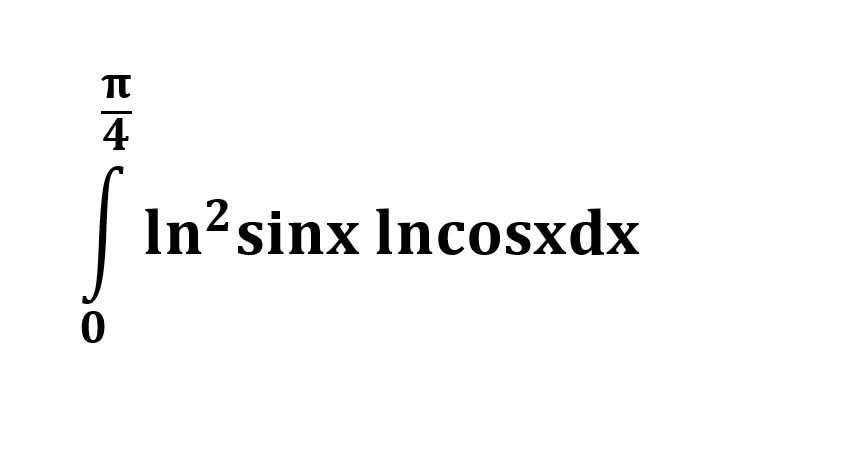
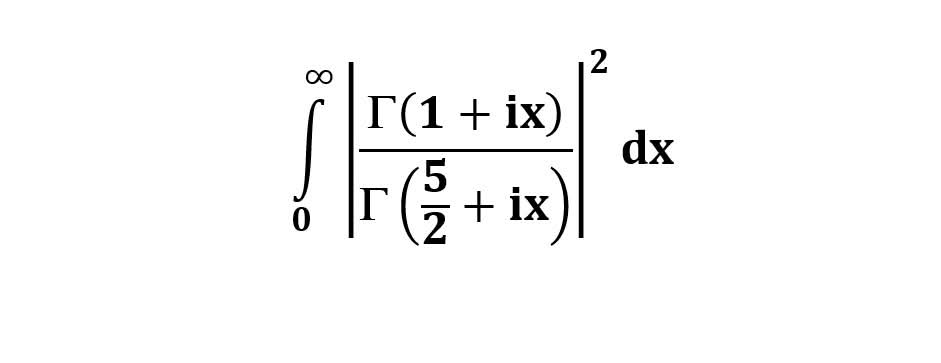
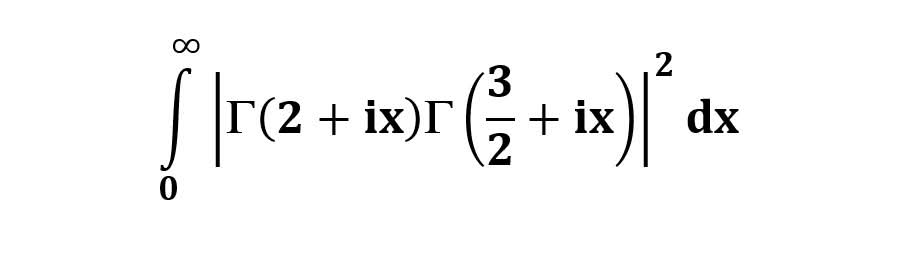
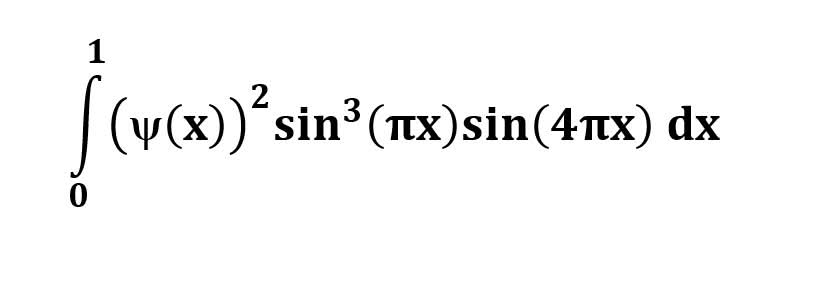
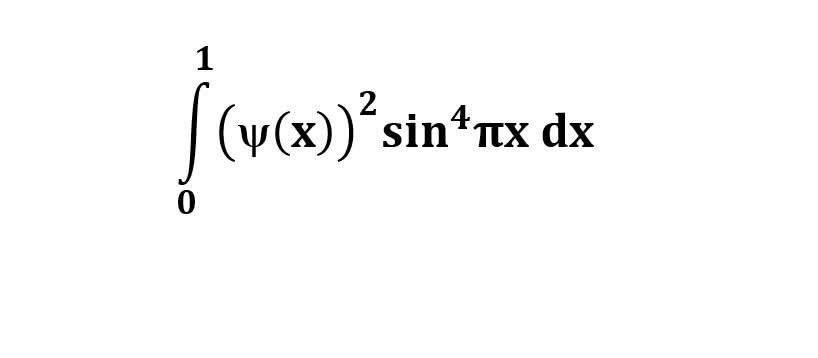
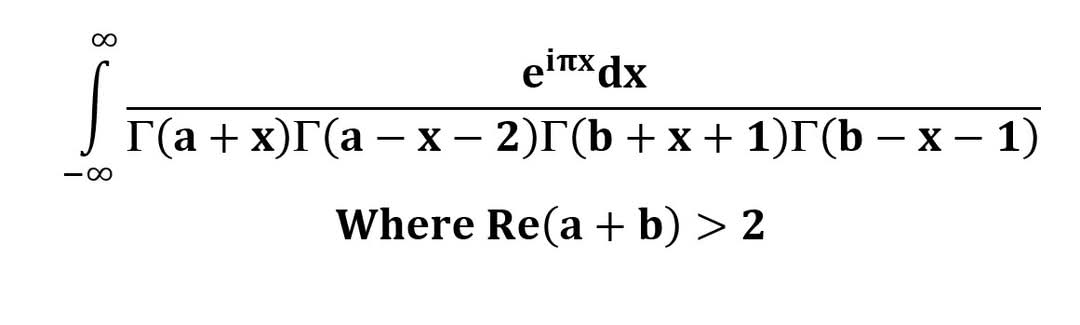
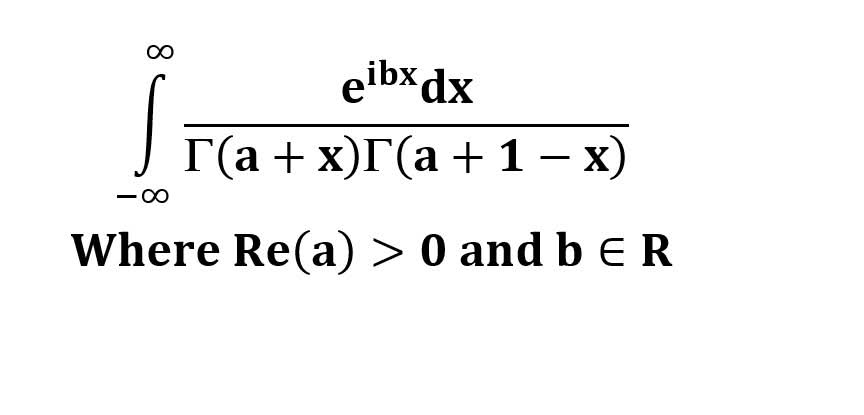
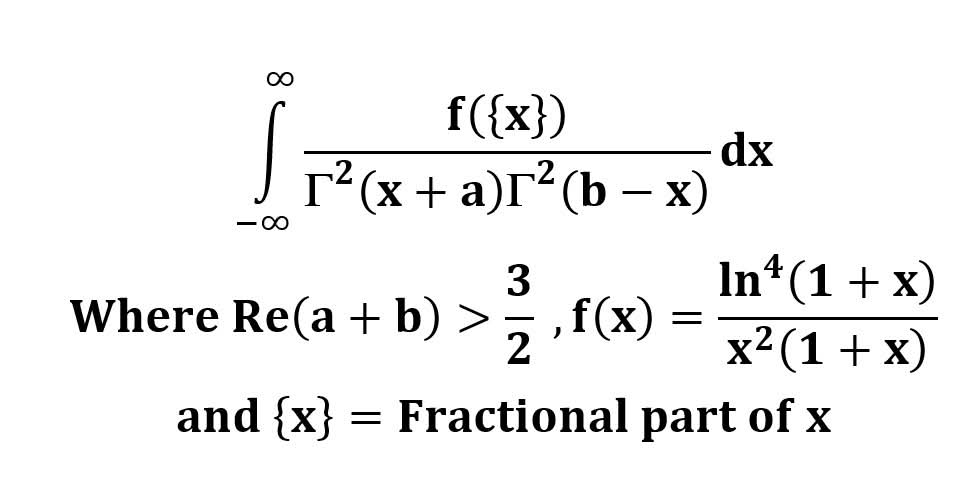
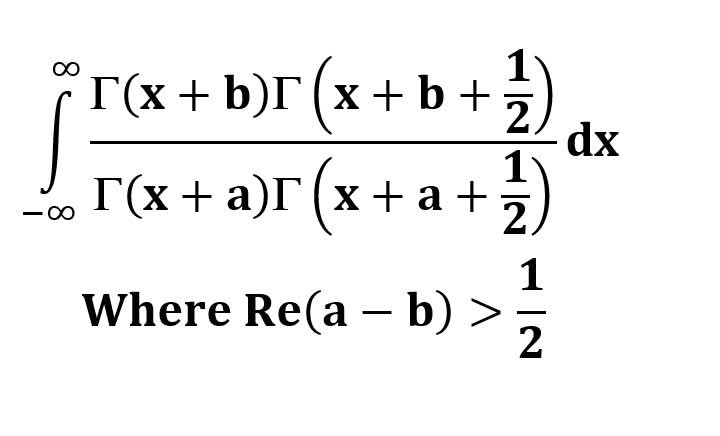
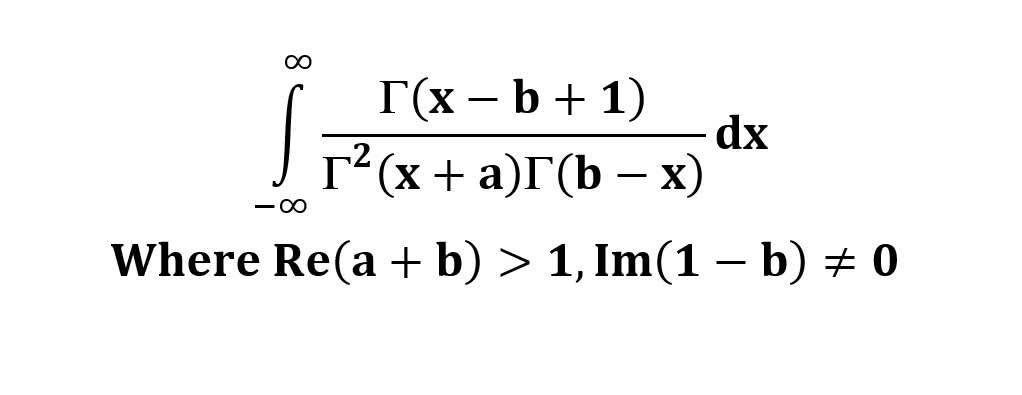
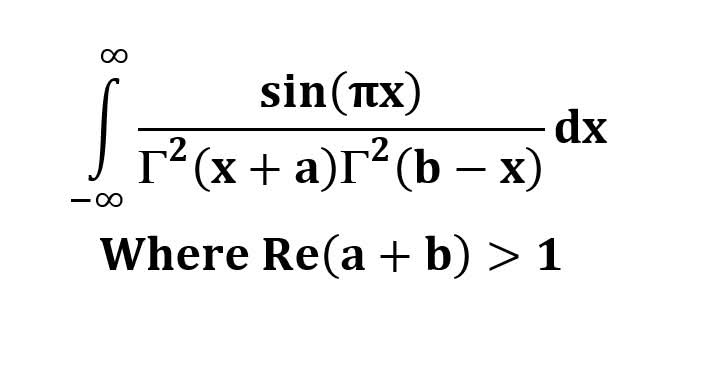
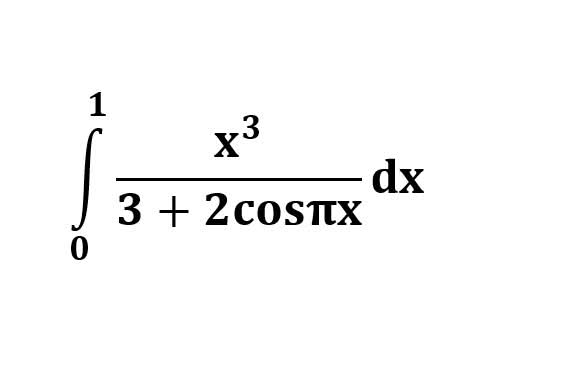
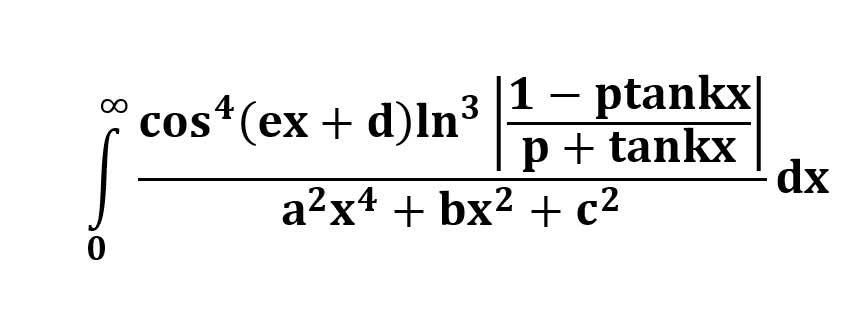
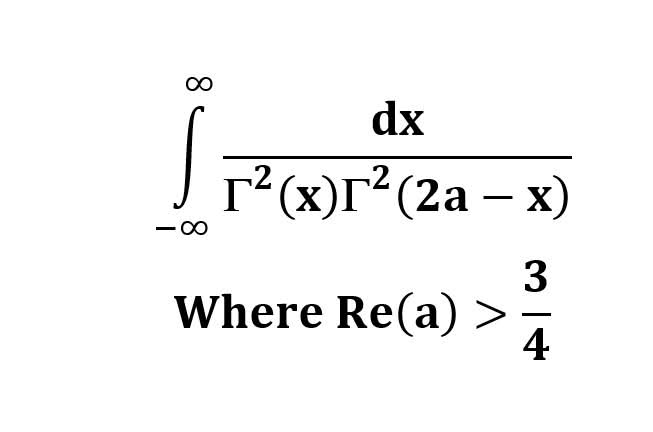
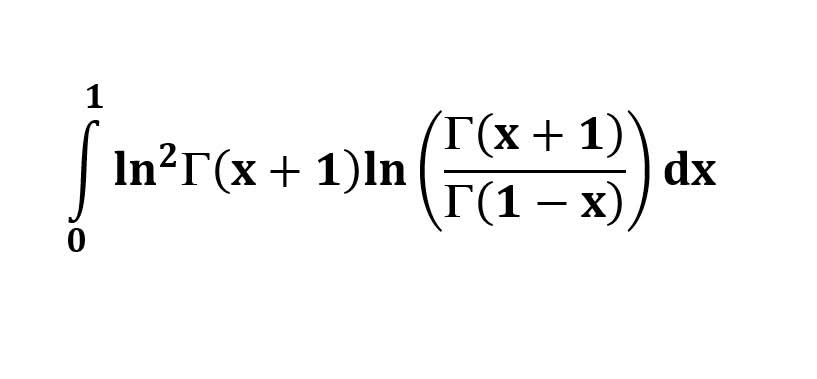
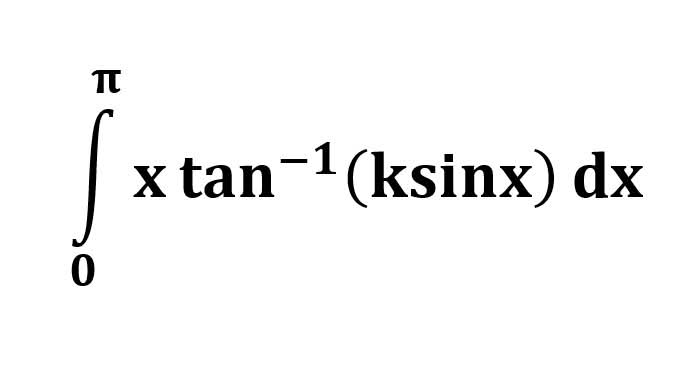
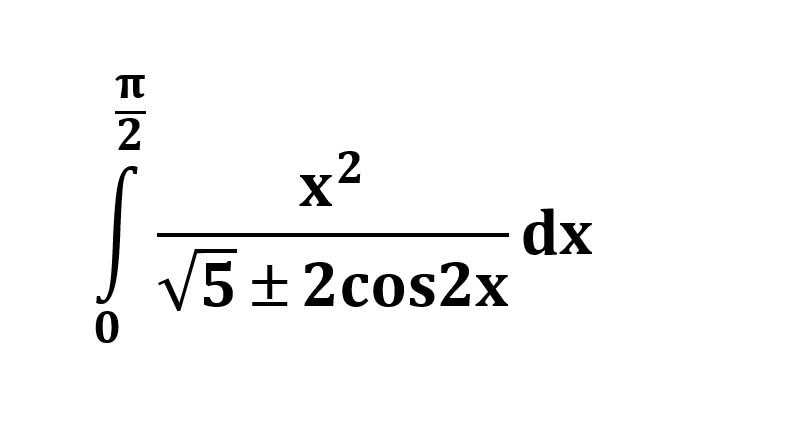
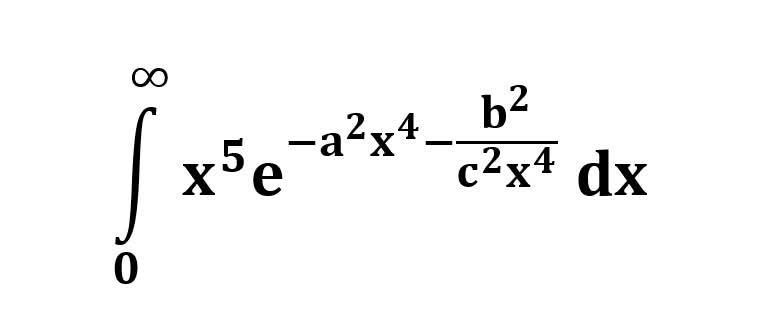
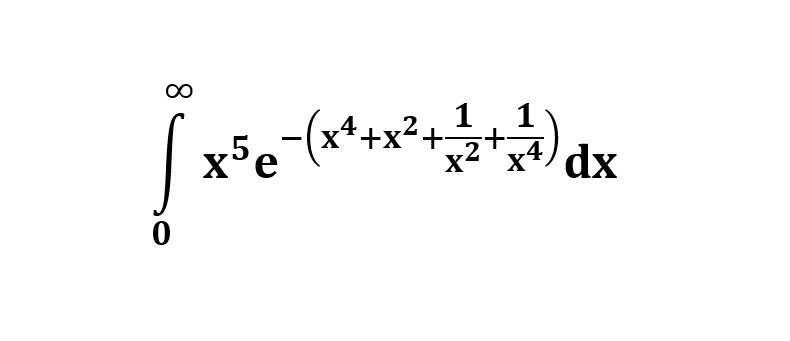
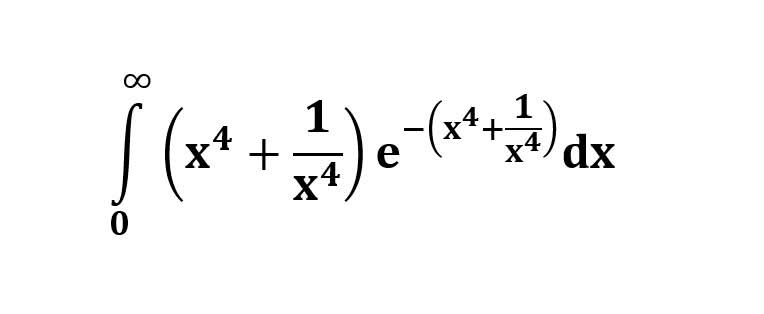
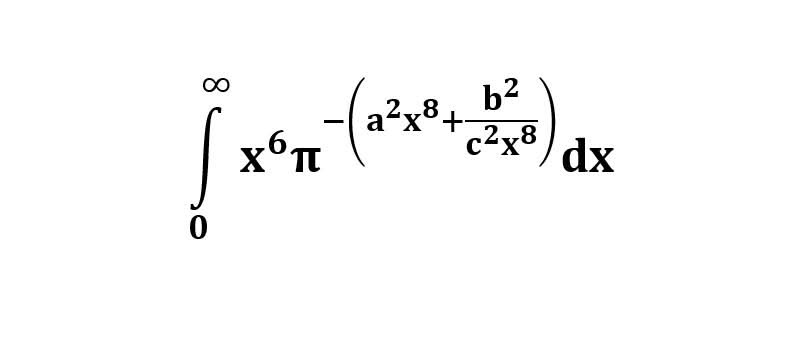
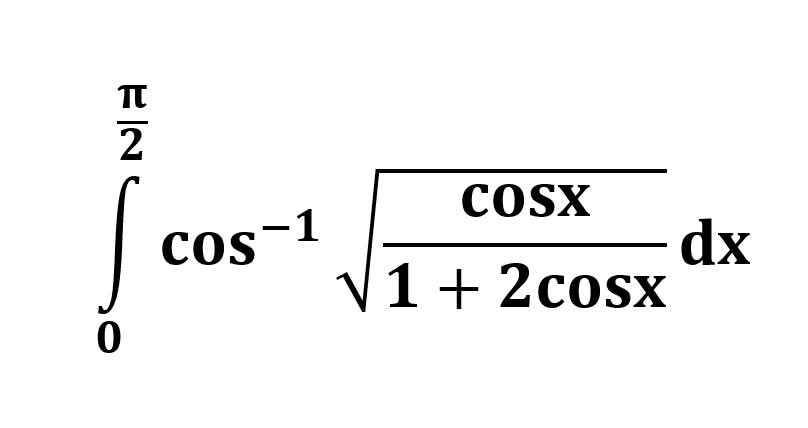
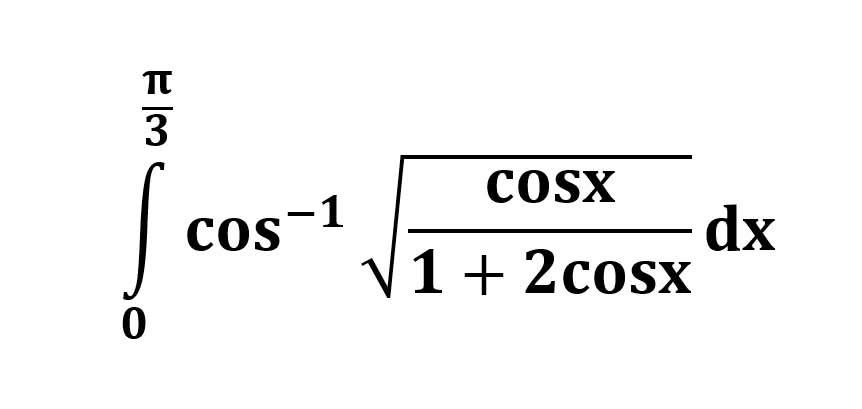
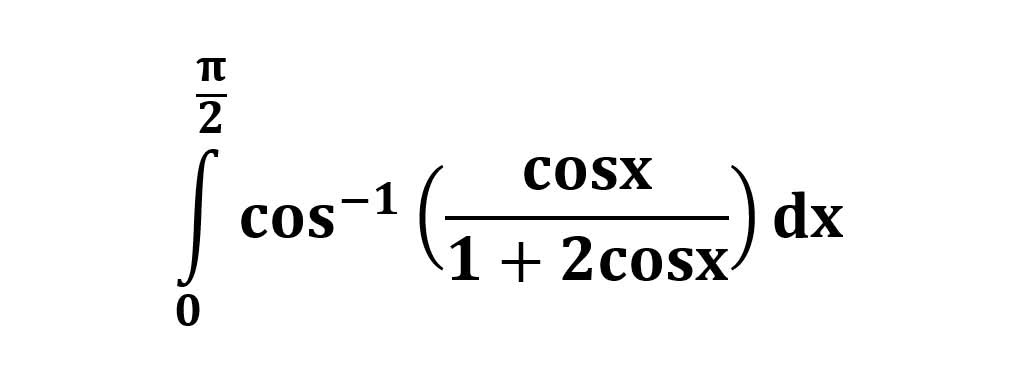
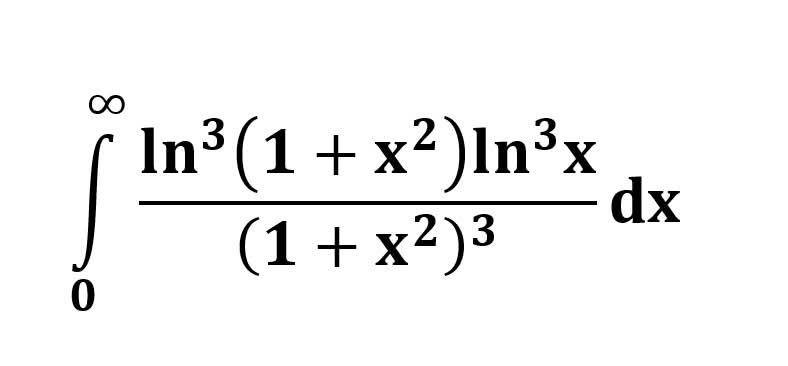
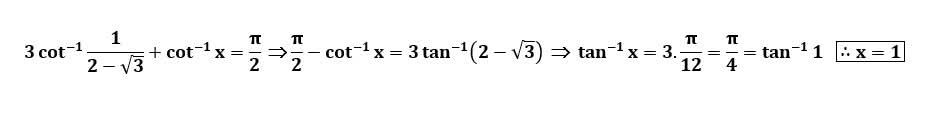
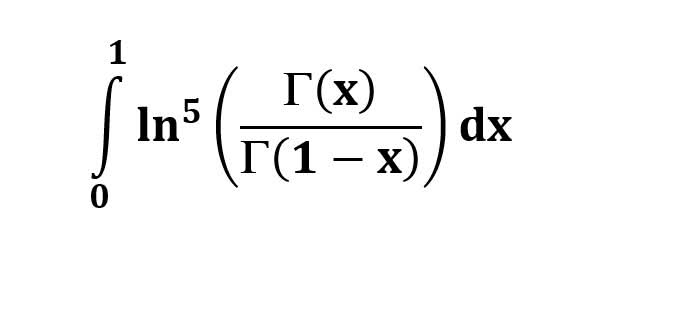
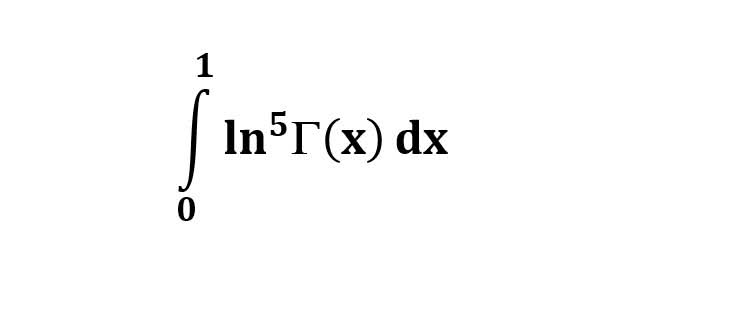
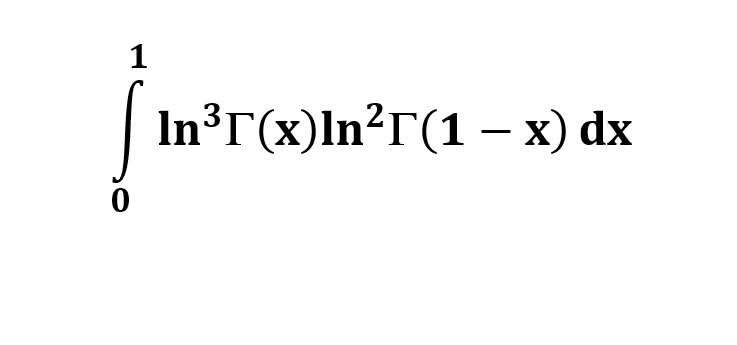
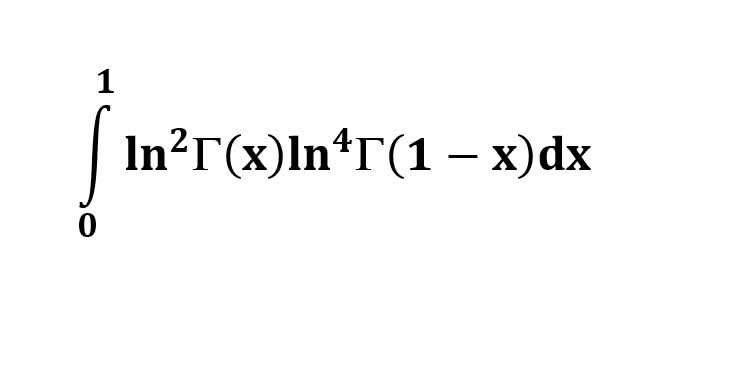
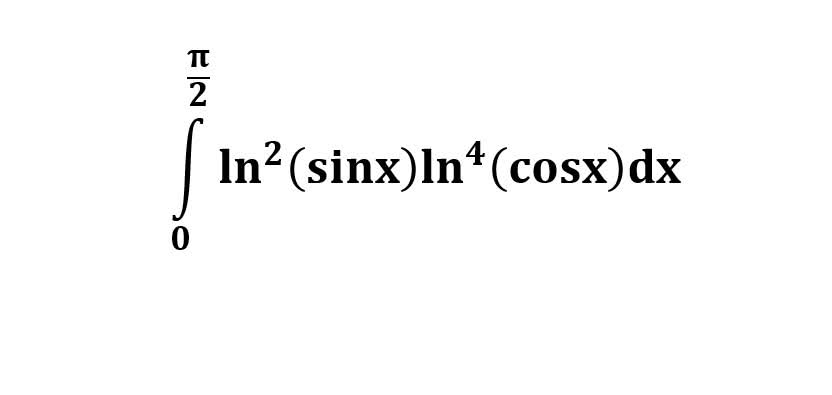
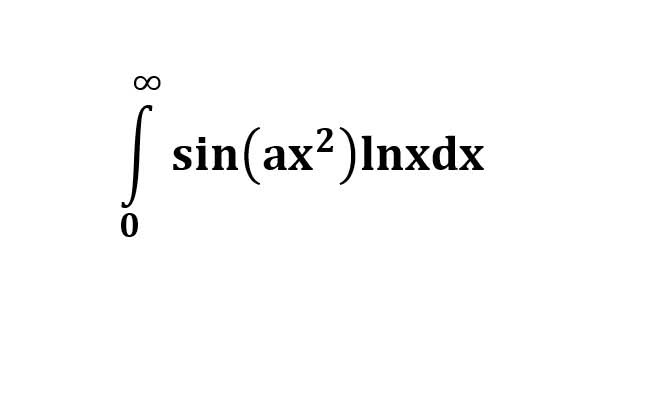
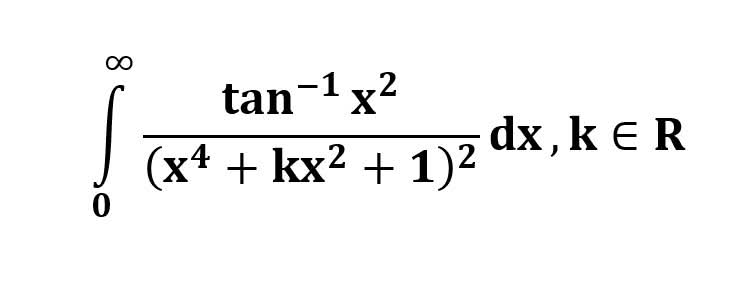
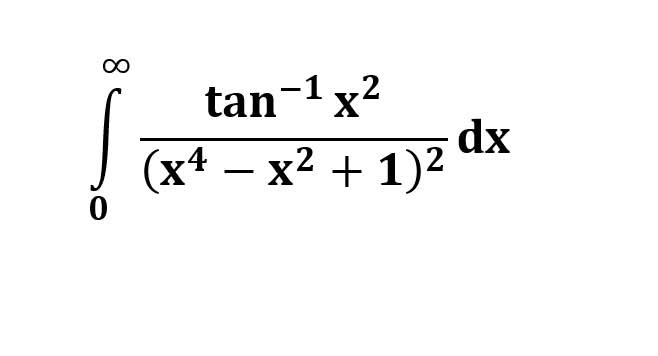
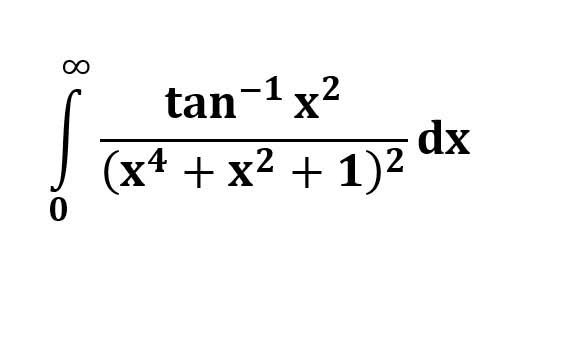
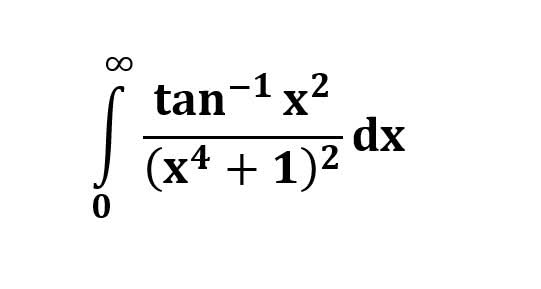
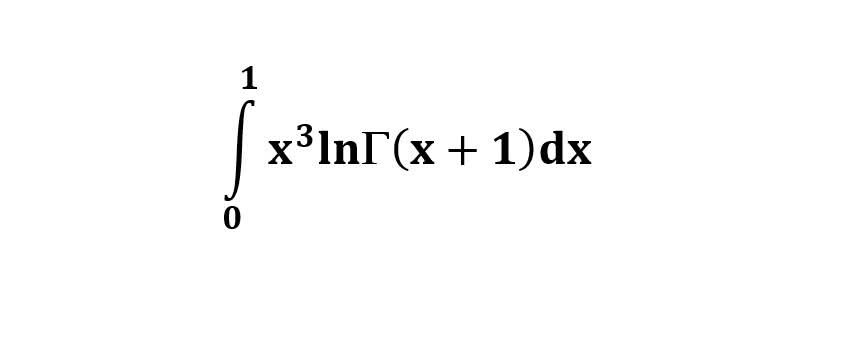
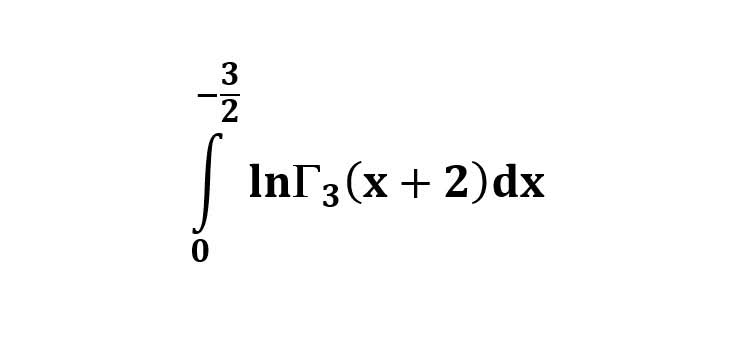
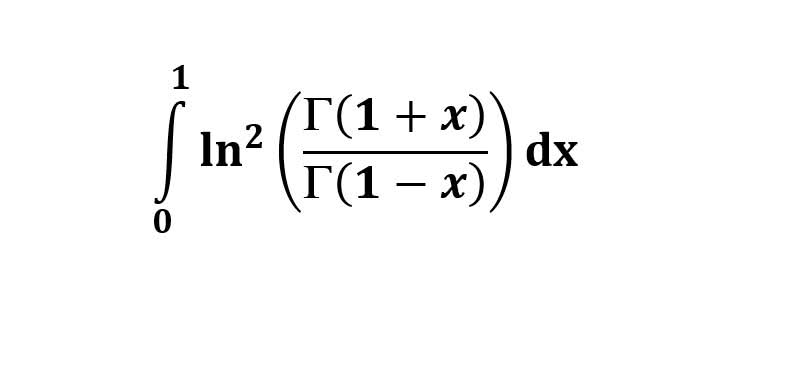
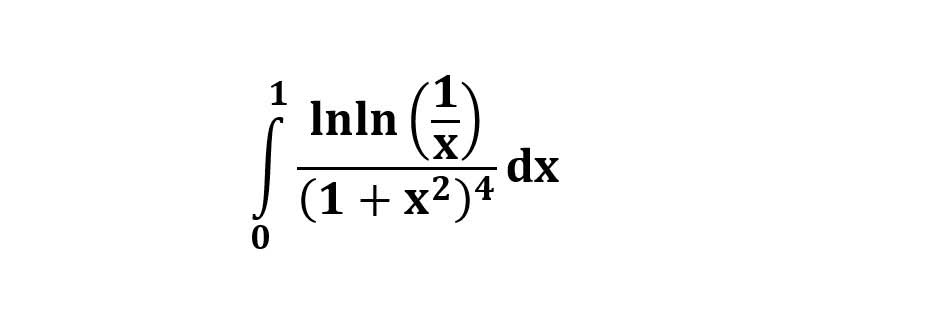
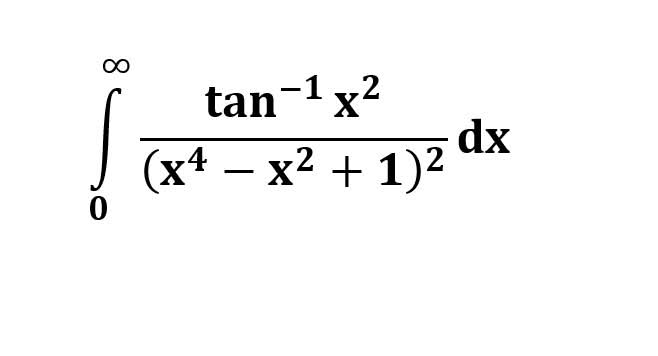
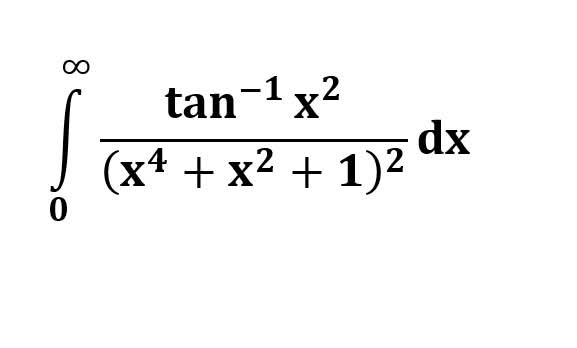
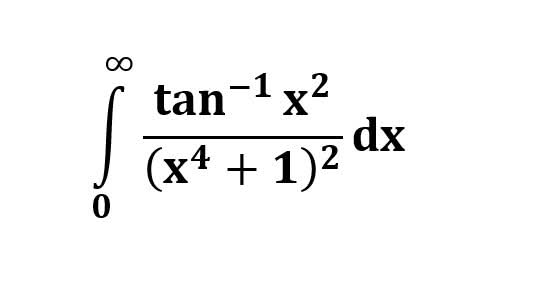
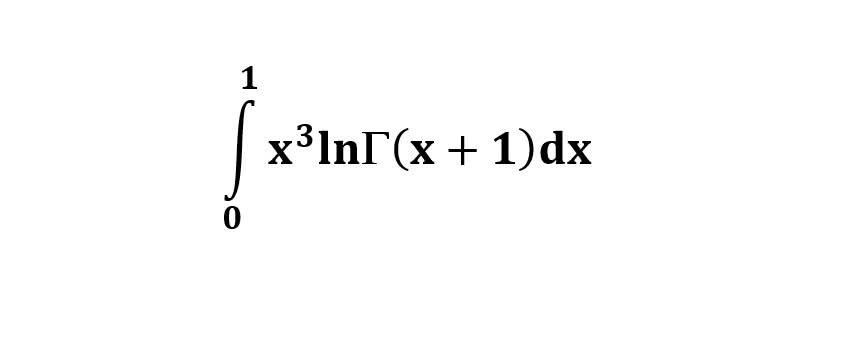

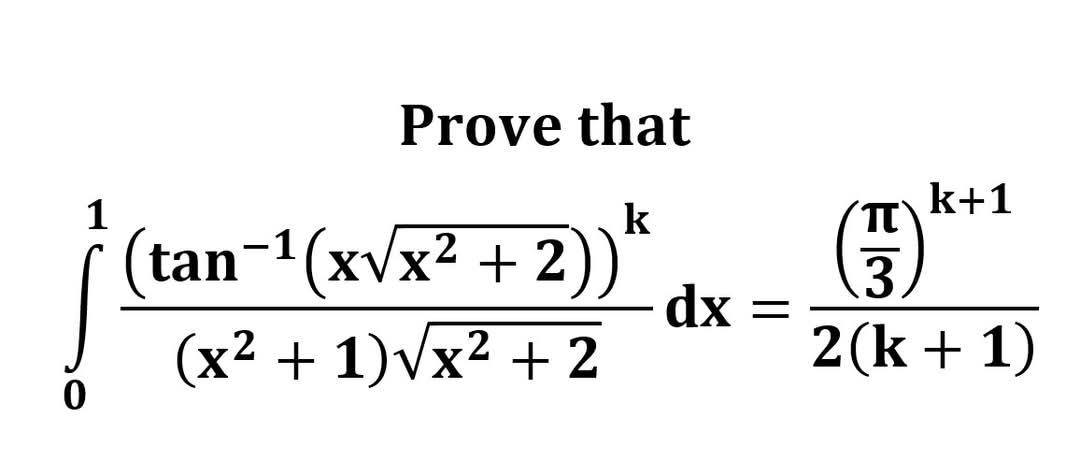
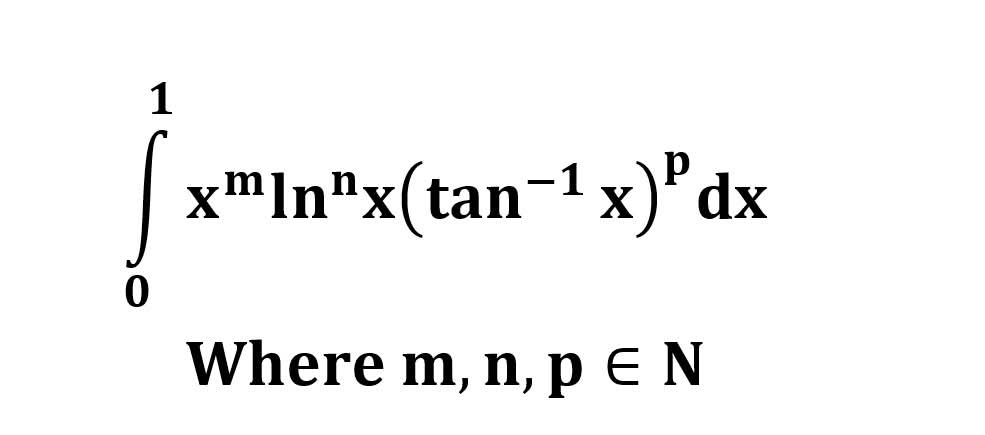
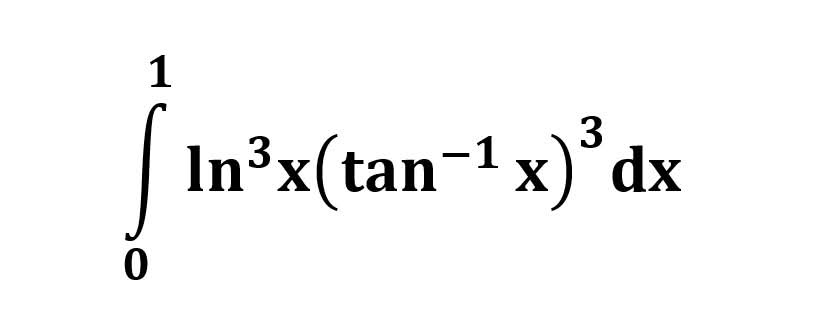
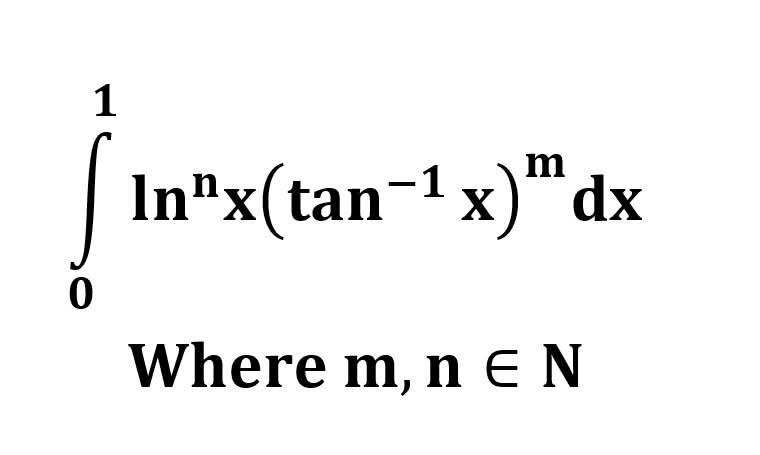
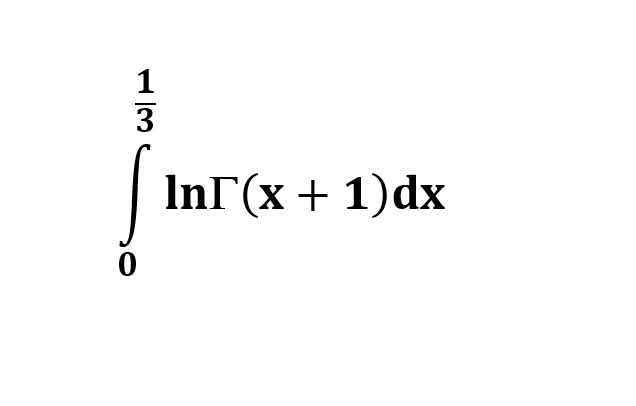
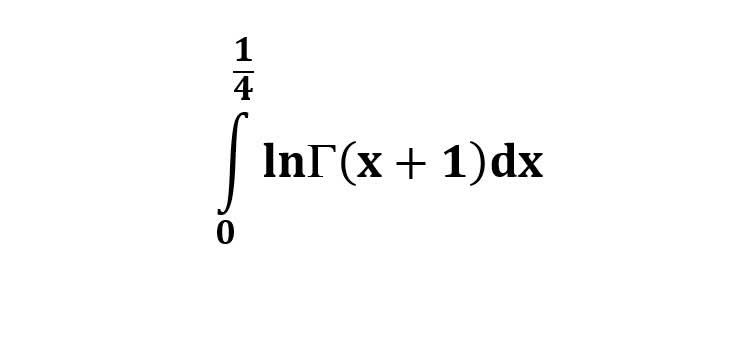
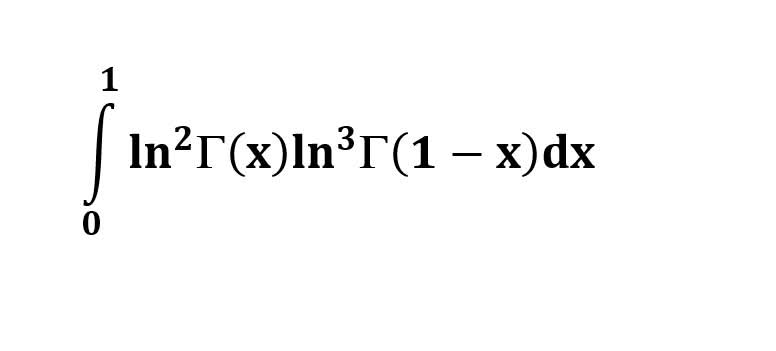
AI가 답을 줄 수 있다. 급하게 해법이 필요한 분은 댓글에 문의바함. ❤️ 사랑과 연민의 다리 ❤️