전기적 퍼텐셜(전위)의 정의
Definition of electrical potential (potential)
아래 이미지는 **전기적 퍼텐셜(전위)**을 정의하고 설명합니다. 핵심 개념은 다음과 같습니다.
- 정의: 전기적 퍼텐셜은 두 물체 사이의 전하 흐름과 단일 물체의 대전 정도를 결정하는 물리량입니다. 이는 전기장 내의 특정 지점까지 무한대에서 단위 양전하를 (가속 없이) 이동시키는 데 필요한 일로 정의되며, 경로에는 무관합니다. 이는 전기장이 보존장이기 때문입니다 (이전 이미지에서 설명됨).
- 계산: 이미지는 점전하 'q'에 의한 'r' 지점에서의 전기적 퍼텐셜(V)을 계산하는 두 가지 동등한 공식을 제공합니다.
- 전기장의 선적분을 사용하는 방법:
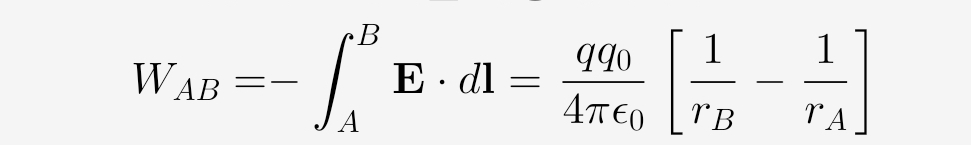
W_{AB} = -\int_A^B \mathbf{E} \cdot d\mathbf{l} = \frac{q q_0}{4\pi \epsilon_0} \left[ \frac{1}{r_B} - \frac{1}{r_A} \right]
여기서 rA는 무한대이고 rB는 'r'입니다.
- 퍼텐셜을 직접 계산하는 방법:
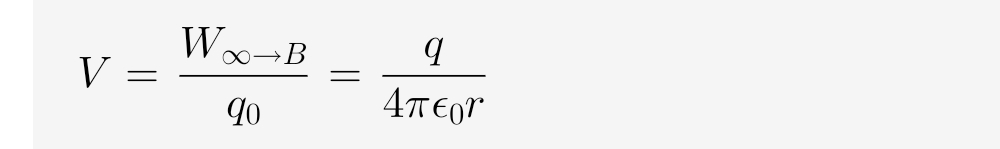
- SI 단위: 전기적 퍼텐셜의 SI 단위는 볼트(V)이며, 이는 쿨롱당 줄(J C⁻¹ ) 또는 쿨롱당 뉴턴미터(N m C⁻¹)와 같습니다.
- 볼트의 정의: 1볼트는 무한대에서 특정 지점까지 1쿨롱의 전하를 이동시키는 데 1줄의 일이 필요한 지점에서의 전기적 퍼텐셜로 정의됩니다.
본질적으로 이 이미지는 점전하의 맥락에서 전기적 퍼텐셜의 정의, 계산, 단위, 그리고 실제 해석을 간결하게 제시하며, 정전기력에 대한 일과의 관계를 강조합니다.

The image presents two methods for calculating electric potential, using the line integral of the electric field and a direct calculation. However, the LaTeX representation in the image is incomplete and contains errors. Here's a corrected and clarified explanation:
1. Using the Line Integral of the Electric Field:
The top equation in the image calculates the work done in moving a test charge from point A to point B using the line integral of the electric field.

W_{AB} = -\int_A^B \mathbf{E} \cdot d\mathbf{l} = \frac{qq_0}{4\pi\epsilon_0} \left[ \frac{1}{r_B} - \frac{1}{r_A} \right]
Where:
- W_{AB}: Work done moving from point A to point B
- \mathbf{E}: Electric field vector
- d\mathbf{l}: Infinitesimal vector along the path
- q: Source charge
- q_0: Test charge
- \epsilon_0: Permittivity of free space
- r_A: Distance from the source charge to point A
- r_B: Distance from the source charge to point B
2. Direct Calculation of Potential:
The bottom equation shows a direct calculation of electric potential. Setting point A at infinity (r_A = \infty) and point B at a distance 'r', we get:
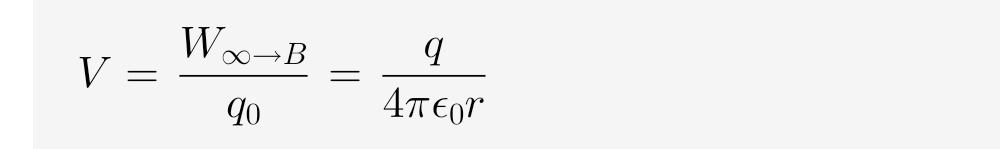
V = \frac{W_{\infty \to B}}{q_0} = \frac{q}{4\pi\epsilon_0 r}
Where:
- V: Electric potential at distance r
- W_{\infty \to B}: Work done moving from infinity to point B
- q_0: Test charge
- q: Source charge
- \epsilon_0: Permittivity of free space
- r: Distance from the source charge to point B
The LaTeX notation in the original image was inaccurate in several places and has been corrected here. The provided explanation is now more precise and easier to understand. The content of the image is now better organized and explained.
예제) 전기 퍼테셜을 직접계산하는 예시
다음은 전기 퍼텐셜을 직접 계산하는 세 가지 예제입니다. 각 예제는 다른 상황과 접근 방식을 보여줍니다.
예제 1: 점전하의 전기 퍼텐셜
- 문제: 전하량이 +2.0 µC인 점전하로부터 5.0 cm 떨어진 지점의 전기 퍼텐셜을 구하시오. (단, 쿨롱 상수 k = 8.99 x 10⁹ Nm²/C²)
- 풀이: 점전하의 전기 퍼텐셜은 다음 식으로 계산됩니다.V = kQ/r여기서,
- V는 전기 퍼텐셜 (볼트)
- k는 쿨롱 상수 (8.99 x 10⁹ Nm²/C²)
- Q는 점전하의 전하량 (2.0 x 10⁻⁶ C)
- r은 점전하로부터의 거리 (0.05 m)
따라서,V = (8.99 x 10⁹ Nm²/C²) * (2.0 x 10⁻⁶ C) / (0.05 m) = 3.6 x 10⁵ V
- 답: +2.0 µC 점전하로부터 5.0 cm 떨어진 지점의 전기 퍼텐셜은 3.6 x 10⁵ V 입니다.
예제 2: 여러 점전하의 전기 퍼텐셜
- 문제: 전하량이 +1.0 µC인 점전하 A와 전하량이 -1.0 µC인 점전하 B가 10 cm 간격으로 떨어져 있습니다. A로부터 5 cm, B로부터 5 cm 떨어진 지점 P의 전기 퍼텐셜을 구하시오.
- 풀이: 여러 점전하의 전기 퍼텐셜은 각 점전하가 만드는 전기 퍼텐셜의 대수적 합으로 계산됩니다.먼저, 점전하 A가 P에서 만드는 전기 퍼텐셜 VA를 계산합니다.VA = kQA/rA = (8.99 x 10⁹ Nm²/C²) * (1.0 x 10⁻⁶ C) / (0.05 m) = 1.8 x 10⁵ V다음으로, 점전하 B가 P에서 만드는 전기 퍼텐셜 VB를 계산합니다.VB = kQB/rB = (8.99 x 10⁹ Nm²/C²) * (-1.0 x 10⁻⁶ C) / (0.05 m) = -1.8 x 10⁵ V따라서, 지점 P의 전체 전기 퍼텐셜 V는 VA와 VB의 합입니다.V = VA + VB = 1.8 x 10⁵ V + (-1.8 x 10⁵ V) = 0 V
- 답: 지점 P의 전기 퍼텐셜은 0 V 입니다.
예제 3: 균일한 전기장 내의 전기 퍼텐셜
- 문제: 전기장의 세기가 1000 V/m인 균일한 전기장 내에서, 두 지점 A와 B 사이의 전위차를 구하시오. A와 B는 20 cm 떨어져 있으며, 전기장 방향과 평행하게 위치해 있습니다.
- 풀이: 균일한 전기장 내에서 두 지점 사이의 전위차는 다음 식으로 계산됩니다.ΔV = -Ed여기서,
- ΔV는 전위차 (볼트)
- E는 전기장의 세기 (1000 V/m)
- d는 두 지점 사이의 거리 (0.2 m)
따라서,ΔV = -(1000 V/m) * (0.2 m) = -200 V
- 답: A와 B 사이의 전위차는 -200 V 입니다. 음수 부호는 전기장 방향으로 이동할 때 전위가 감소함을 나타냅니다.
이 세 가지 예제는 전기 퍼텐셜 계산의 기본적인 원리를 보여줍니다. 더 복잡한 상황에서는 적분을 사용하여 전기 퍼텐셜을 계산해야 할 수 있습니다.