단일 점 전하에 의한 퍼텐셜

  Potential by single point charge
(수식은 LaTeX 형태로도 2중 표현되어 있습니다.)
  
  단일 점전하 +q로부터 거리 x에 위치한 시험 전하 +q_0을 고려해 봅시다. 시험 전하에 작용하는 정전기적 힘은 쿨롱의 법칙에 의해 다음과 같이 주어집니다.

\vec{F} = +q_0 \vec{E}

여기서 \vec{E}는 점전하 +q에 의한 전기장입니다. 이 힘은 방사형으로 바깥쪽으로 향하며 시험 전하를 가속시키려는 경향이 있습니다. 이 가속을 방지하기 위해, -q_0 \vec{E}와 같은 크기의 반대 방향 힘을 가해야 합니다.

이 힘에 대항하여 시험 전하를 미소 거리 dx만큼 이동시키는 데 드는 일 (dW)은 다음과 같습니다.

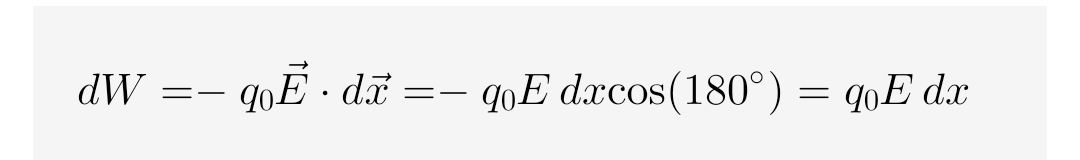
dW = -q_0 \vec{E} \cdot d\vec{x} = -q_0 E \, dx \cos(180^\circ) = q_0 E \, dx

점전하에 의한 전기장은 다음과 같습니다.

E = \frac{q}{4\pi\epsilon_0 x^2}


이것을 dW에 대한 식에 대입하면 다음과 같습니다.

dW = \frac{q q_0}{4\pi\epsilon_0 x^2} dx

시험 전하를 무한대 (\infty)에서 점전하로부터 거리 r까지 이동시키는 데 드는 총 일 (W_{\infty B})을 구하기 위해 적분을 수행합니다.

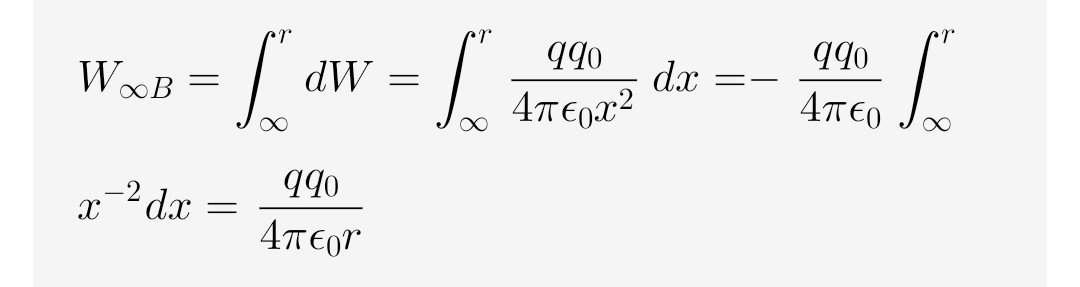
W_{\infty B} = \int_{\infty}^{r} dW = \int_{\infty}^{r} \frac{q q_0}{4\pi\epsilon_0 x^2} dx = -\frac{q q_0}{4\pi\epsilon_0} \int_{\infty}^{r} x^{-2} dx = \frac{q q_0}{4\pi\epsilon_0 r}

점전하 +q로부터 거리 r에서의 전위 (V)는 무한대에서 그 점까지 시험 전하를 가져오는 데 드는 단위 전하당 일로 정의됩니다.

V = \frac{W_{\infty B}}{q_0} = \frac{q}{4\pi\epsilon_0 r}

이 공식적인 제시는 점전하에 의한 전위의 유도 과정을 명확하게 보여주며, 관련된 물리적 원리와 수학적 단계를 강조합니다. 벡터 표기법 (\vec{F}, \vec{E}, d\vec{x})의 사용은 원본 이미지의 스칼라 표현보다 더 엄밀합니다.

Potential by single point charge

The following presents the equations from the image in a more formal, paper-like format, using LaTeX for mathematical notation.

Electric Potential due to a Single Point Charge

Consider a test charge, +q_0, located at a distance x from a source charge, +q.  The electrostatic force acting on the test charge is given by Coulomb's law:

\vec{F} = +q_0 \vec{E}

where \vec{E} is the electric field due to the source charge +q.  This force is radially outward, tending to accelerate the test charge. To prevent this acceleration, an equal and opposite force, -q_0 \vec{E}, must be applied.

The work done (dW) in moving the test charge an infinitesimal distance dx against this applied force is:

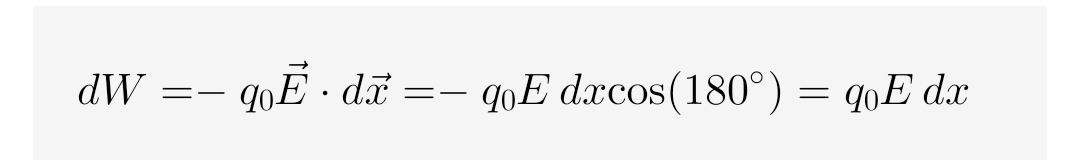
dW = -q_0 \vec{E} \cdot d\vec{x} = -q_0 E \, dx \cos(180^\circ) = q_0 E \, dx


The electric field due to a point charge is:

E = \frac{q}{4\pi\epsilon_0 x^2}


Substituting this into the expression for dW:

dW = \frac{q q_0}{4\pi\epsilon_0 x^2} dx

To find the total work done (W_{\infty B}) in moving the test charge from infinity (\infty) to a distance r from the source charge, we integrate:

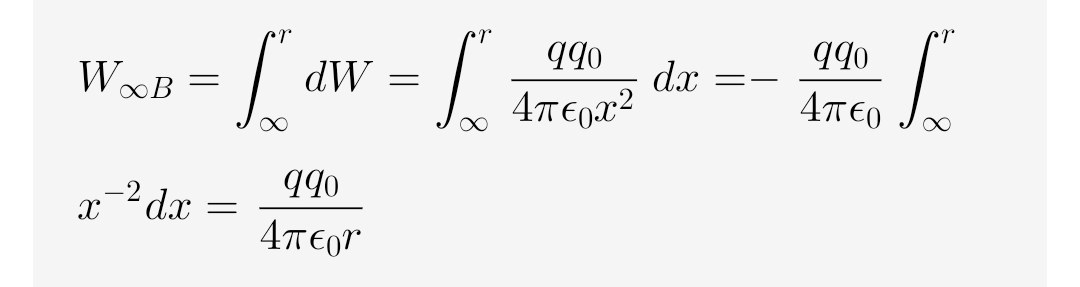
W_{\infty B} = \int_{\infty}^{r} dW = \int_{\infty}^{r} \frac{q q_0}{4\pi\epsilon_0 x^2} dx = -\frac{q q_0}{4\pi\epsilon_0} \int_{\infty}^{r} x^{-2} dx = \frac{q q_0}{4\pi\epsilon_0 r}


The electric potential (V) at a distance r from a point charge +q is defined as the work done per unit charge in bringing a test charge from infinity to that point:

V = \frac{W_{\infty B}}{q_0} = \frac{q}{4\pi\epsilon_0 r}

This formal presentation clarifies the derivation of the electric potential due to a point charge, emphasizing the physical principles and mathematical steps involved.  The use of vector notation (\vec{F}, \vec{E}, d\vec{x}) is more rigorous than the scalar representation in the original image.