파동, 파동 방정식 및 입자 속도의 기본 특성
Basic properties of waves, wave equations, and particle velocities
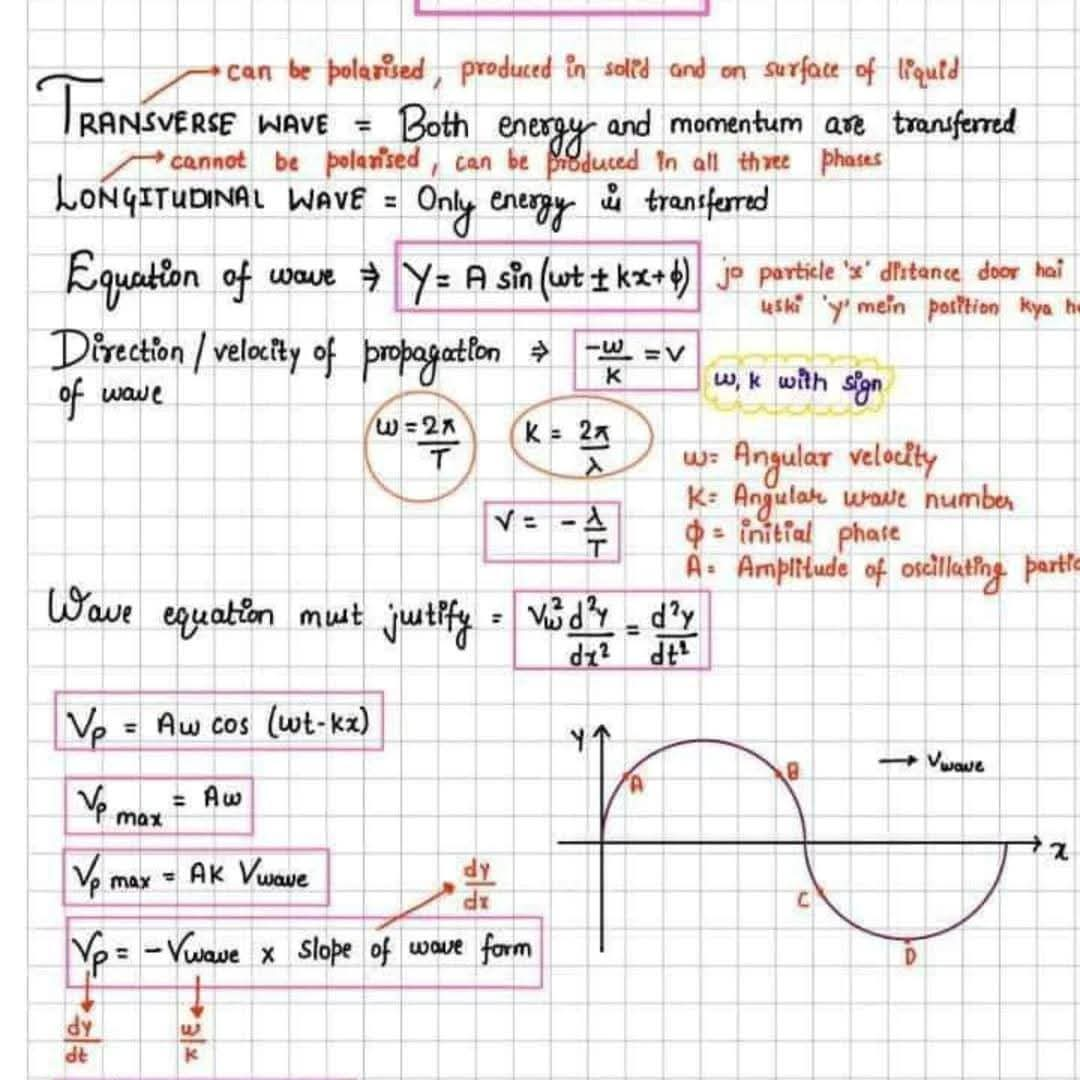
1. 횡파와 종파의 비교:
- 횡파 (Transverse Wave): 에너지와 운동량 모두 전달되며, 편광될 수 있고 고체 및 액체 표면에서 발생합니다.
- 종파 (Longitudinal Wave): 에너지만 전달되며, 편광될 수 없고 세 가지 상(고체, 액체, 기체) 모두에서 발생합니다.
2. 파동 방정식:
- 일반적인 파동 방정식: Y = A sin(ωt ± kx + φ)
- 여기서:
- A : 진폭 (Amplitude)
- ω : 각속도 (Angular velocity)
- k : 파수 (Angular wave number)
- φ : 초기 위상 (Initial phase)
- t : 시간
- x : 위치
- 파동의 진행 방향/속도: v = ω/k (단, ω와 k의 부호를 고려해야 함)
- 각속도와 파수: ω = 2π/T (T는 주기), k = 2π/λ (λ는 파장)
- 파동 방정식의 조건: v² ∂²y/∂x² = ∂²y/∂t² (파동 방정식은 이 식을 만족해야 함)
3. 입자 속도:
- 입자 속도 (Particle Velocity, Vp): Vp = Aw cos(ωt - kx)
- 최대 입자 속도: Vp_max = Aw
- 입자 속도와 파동 속도의 관계: Vp_max = AkVwave
- 입자 속도와 파형 기울기의 관계: Vp = -Vwave * (dy/dx) (dy/dx는 파형의 기울기)
4. 그래프:
그래프는 파동의 형태를 보여주는 것으로 보입니다. A, B, C, D는 파동의 특정 시점을 나타내는 것으로 추정됩니다. x축은 위치, y축은 변위를 나타냅니다. 화살표는 파동의 진행 방향을 나타냅니다.
요약: 이 이미지는 파동의 기본적인 특성, 파동 방정식, 그리고 입자 속도에 대한 설명을 담고 있습니다. 횡파와 종파의 차이점과 파동 방정식의 조건을 명확하게 제시하고 있으며, 그래프를 통해 파동의 형태를 시각적으로 보여줍니다. 물리학, 특히 파동에 대한 기본적인 이해를 돕는 자료로 볼 수 있습니다.
이미지의 그래프에서 A, B, C, D는 무엇을 나타내는 건가요?
이미지의 그래프에서 A, B, C, D는 파동의 한 주기 동안의 특정 시점을 나타냅니다. 더 자세히 설명하면 다음과 같습니다.
- A: 파동이 평형 위치(y=0)에서 최대 양의 변위를 가지는 지점입니다. 이 시점에서 입자는 위쪽으로 최대 속도를 가지고 있습니다.
- B: 파동이 최대 양의 변위에서 평형 위치로 이동하는 중간 지점입니다. 이 시점에서 입자의 속도는 감소하고 있고, 가속도는 음의 값을 가집니다.
- C: 파동이 평형 위치에서 최대 음의 변위를 가지는 지점입니다. 이 시점에서 입자는 아래쪽으로 최대 속도를 가지고 있습니다.
- D: 파동이 최대 음의 변위에서 평형 위치로 이동하는 중간 지점입니다. 이 시점에서 입자의 속도는 감소하고 있고, 가속도는 양의 값을 가집니다.
결론적으로 A, B, C, D는 파동의 진행 방향에 따라 주기적인 변위 변화를 보여주는 대표적인 네 지점입니다. 각 지점에서 입자의 변위, 속도, 가속도는 모두 다릅니다.
Basic properties of waves, wave equations, and particle velocities
The image above shows some of the physics lecture notes on waves. The main contents are as follows:
1. Comparison of lateral and sectarian:
- Transverse Wave: Both energy and momentum are transferred, can be polarized and occur on solid and liquid surfaces.
- Longitudinal Wave: Only energy is transmitted, cannot be polarized and occurs in all three phases (solid, liquid, gas).
2. Wave equation:
- General wave equation: Y = A sin(ωt ± kx + φ)
- Here:
- A: Amplitude
- ω: Angular velocity
- k: Angular wave number
- φ: Initial phase
- t: Time
- x: Location
- Direction/speed of the wave: v = ω/k (however, signs of ω and k must be considered)
- Angular velocity and wave number: ω = 2π/T (T is period), k = 2π/λ (λ is wavelength)
- Conditions of wave equation: v2 ∂2y/∂x2 = ∂2y/∂t2 (wave equation must satisfy this equation)
3. Particle velocity:
- Particle velocity (Particle Velocity, Vp): Vp = Aw cos(ωt - kx)
- Maximum particle velocity: Vp_max = Aw
- Relationship between particle velocity and wave velocity: Vp_max = AkVwave
- Relationship between particle velocity and waveform slope: Vp = -Vwave * (dy/dx) (dy/dx is the slope of the waveform)
4. Graph:
The graph appears to show the shape of the wave; A, B, C, and D are presumed to represent a specific time point of the wave; the x-axis represents the position, the y-axis represents the displacement; and the arrows indicate the direction of the wave's progress.
Summary: This image contains descriptions of the basic characteristics of waves, wave equations, and particle velocities. It clearly presents the differences between transverse waves and longitudinal waves and the conditions of wave equations, and visually shows the shape of waves through graphs. It can be seen as data to help basic understanding physics, especially waves.
What do A, B, C, and D represent in the graph of the image?
In the graph of the image, A, B, C, and D represent a specific time point during a period of wave; in more detail, it follows:
- A: The point where the wave has a maximum positive displacement at equilibrium position (y=0). At this point the particle has a maximum velocity upwards.
- B: The midpoint where the wave moves from maximum positive displacement to equilibrium position. At this point, the velocity of the particle is decreasing, and the acceleration has a negative value.
- C: The point where the wave has a maximum negative displacement at its equilibrium position. At this point the particle has a maximum velocity downward.
- D: Midpoint where the wave moves from maximum negative displacement to equilibrium position. At this point, the velocity of the particles is decreasing, and the acceleration has a positive value.
In conclusion, A, B, C, and D are four representative points showing periodic displacement changes depending on the direction of the wave's progress; at each point, the displacement, velocity, and acceleration of the particles are all different.