비가역성 추력에서 시공간 격자출현
Spacetime lattice appearance at non-angle-reversible thrust
."비가역성 추력에서 시공간 격자 출현"을 쉬운 한글로 풀어쓰면 다음과 같습니다:
- - 되돌릴 수 없는 힘이 만들어내는 시공간 그물
- - 시간과 공간의 그물은 되돌아갈 수 없는 힘에서 시작된다
- - 되돌릴 수 없는 힘으로부터 나타나는 시간과 공간의 구조
- - 되돌릴 수 없는 힘이 시공간을 그물처럼 만든다
개념요약
시공간 격자는 시간과 공간을 연결하여 표현하는 일종의 "지도" 또는 "구조"라고 생각할 수 있습니다. 좀 더 자세히 설명하면 다음과 같습니다.
- 기본 개념:
- 시공간 (Spacetime): 아인슈타인의 상대성 이론에서 시간과 공간은 분리된 개념이 아니라 서로 얽혀 하나의 연속체를 이룬다고 봅니다. 이를 시공간이라고 부릅니다.
- 격자 (Lattice): 격자는 규칙적으로 배열된 점들의 집합입니다. 마치 바둑판이나 그래프 용지처럼 일정한 간격으로 선들이 교차하는 형태를 떠올리면 됩니다.
- 시공간 격자의 의미:
- 시공간을 표현하는 틀: 시공간 격자는 이 시공간을 시각적으로 표현하고 분석하기 위한 도구입니다. 우주의 구조, 중력, 입자들의 움직임 등을 이해하는 데 도움을 줍니다.
- 우주의 기본 구조: 일부 이론에서는 시공간 자체가 연속적인 것이 아니라, 아주 작은 "알갱이"들로 이루어진 격자 형태일 수 있다고 주장합니다. 이는 마치 우리가 보는 매끄러운 화면이 실제로는 아주 작은 픽셀들로 구성된 것과 같습니다.
- 예시:
- 영화 속 워프: 영화에서 우주선이 워프를 할 때 화면에 나타나는 구부러진 격자 무늬가 시공간 격자를 시각적으로 표현한 것입니다.
- 블랙홀 주변의 시공간: 블랙홀 주변에서는 중력이 매우 강해 시공간이 심하게 휘어집니다. 이를 시공간 격자로 표현하면 격자선들이 블랙홀 쪽으로 심하게 굽어지는 모습을 볼 수 있습니다.
- 핵심:
- 시공간 격자는 시간과 공간을 연결하여 표현하는 도구입니다.
- 우주의 구조, 중력, 입자들의 움직임 등을 이해하는 데 도움을 줍니다.
- 일부 이론에서는 시공간 자체가 격자 형태일 수 있다고 주장합니다.
즉, 시공간 격자는 우주를 더 잘 이해하기 위한 "지도" 또는 "구조"이며, 이는 우리가 사는 세계를 더 깊이 파고드는 데 중요한 역할을 합니다.
통일된 작용을 향한 길: 힐베르트 원, 기능적 정보, 행렬 연산자를 통한 역학의 일반 이론
Daniel Joseph Betro
2025년 8월 30일
초록
우리는 단일 라그랑주 밀도(Lagrangian density)가 다음과 같이 결합되는 통일된 결정론적 장 이론(deterministic field theory)을 제시합니다. (i) 블록 중앙화 장치가 표준 모델 게이지 대수(Standard Model gauge algebra)를 산출하는 비섭동 행렬/연산자 필드 M; (ii) 근접 타격(near-hits)에서 구별되는 각도가 로그 불변 방식으로 국소 등각 구동(local conformal driving)을 통해 기능적 정보 스칼라 F에 연결하는 "힐베르트 시계"인 힐베르트 원 상태 Ψ(x,s); (iii) 접근 가능한 에너지를 로그 불변 방식으로 정보에 연결하는 I(E) = M(E) ln(E/E₀); (iv) 엄격한 국소성과 적절한 쌍곡성을 보장하는 메트릭 풀백(metric pullback); (v) (3,2,1) 시그니처(signature)를 갖는 블록 대각 M에 대한 헤세 행렬(Hessian)에서 발생하는 운동학적 정규화(kinetic normalizations)를 갖는 게이지/물질 섹터(gauge/matter sectors). 우리는 명시적인 오일러-라그랑주 방정식(Euler-Lagrange equations), 중앙화 장치를 su(3) ⊕ su(2) ⊕ u(1) 양자화(quantization)의 필드 방정식, 유도체 연결, 요동의 통계적 검증 및 절제(ablations), 임계값을 갖는 재정규화 그룹 복도(renormalization-group corridors)를 제공합니다. 우리는 LEE-인식 통찰력 실험(LEE-aware thought experiments) - 힐베르트 원, 강화/동기화(reinforcement/synchronization), 빅뱅 추력(Big Thrust)(전/후 빅뱅 전환), 규모 의존적 관찰(scale-dependent observation) 및 국소성 보존(Conservation of Locality)을 개발하고, 이제 엄격한 수학 내에서 구성된 지침과 동일한 언어로 구성합니다.
목차
1. 서론 및 핵심 원리 2
2. 통일된 라그랑주 및 필드 방정식 3
2.1 작용 및 섹터 3
2.2 오일러-라그랑주 방정식 3
2.3 콤팩트 연산자 아인슈타인 유사 방정식 4
2.4 (3,2,1)의 중앙화 장치에서 SM 출현 4
3. 사고 실험: 확장된 서사적 기반 4
3.1 힐베르트 원 및 근접 타격 4
3.2 강화 및 동기화 5
3.3 빅뱅 추력 (전/후 빅뱅 전환) 5
3.4 규모 의존적 관찰 5
3.5 국소성 보존 5
4. 기능적 정보: 에너지 연결, 로그 불변 구동자 5
4.1 정의 및 근거 5
4.2 기본 속성 6
1
2. 통일된 라그랑주 및 필드 방정식
2.1 작용 및 섹터
우리는 시그니처(-, +, +, +)를 갖는 로렌츠 메트릭 gμν, 행렬/연산자 필드 M(x), 힐베르트 원 필드 Ψ(x, s) ∈ H 와 s ∈ [-1, 1] 및 표준 게이지/물질 내용물 (Aμ, ψ, H,...)을 취합니다. 작용은
S = ∫ d⁴x √-g Ltotal = ∫ d⁴x √-g (LM + Lψ + Linfo + Lgauge + Lmatter + Lpull) (1)
대표적인 구성 요소는 다음과 같습니다.
LM = ½ Tr((∇M)ᵀ(∇M)) - V(M), (2)
Lψ = ∫ds (<Ψ|K̂(s)|Ψ> - U(Ψ)), (3)
-1
Linfo = αI I(E) + αK ∫ds (<Ψ|K̂(s)|Ψ>), I(E) = M(E) ln(E/E₀) (4)
-1
Lgauge = -∑ 1/4ga² F(a)μν F(a)μν + ... (5)
a=1
Lmatter = ψ(iγμDμ - yH)ψ + (DμH)†(DμH) - λ(|H|² - v²)² + ... (6)
Lpull = ½ R[g] - ½ (∇μ∇ν - gμν□) ln F(I, K, Γ) gμν. (7)
여기서 K(x) := ∫ds (Ψ|K̂(s)|Ψ) 는 구별되는 각도에서 근접 타격 밀도를 인코딩합니다. E는 국소 스칼라 에너지 또는 에너지 밀도입니다. E₀는 정보 제로로 설정합니다. 부드러운 양의 F는 등각 구동기를 생성하고, *Γ*는 나중에 도입될 느린 강화/동기화 필드입니다.
2.2 오일러-라그랑주 방정식
(1)을 변화시키면 다음이 주어집니다.
-Gμν[g] = TμνM + Tμνψ + Tμνinfo + Tμνgauge + Tμνmatter - ½ (∇μ∇ν - gμν□) ln F(I, K, Γ), (8)
-□M + ∂V/∂M = Jm(Ψ, gauge, matter), (9)
K̂(s)|δU/δ(Ψ)> = -αK K̂(s)|Ψ>, s ∈ [-1, 1], (10)
δI/δE = M'(E)/M(E) I(E) + 1/E₀ δln F/δE ∝ αI 1/E. (11)
등각 연산자 (∇μ∇ν - gμν□) ln F는 2차 및 로컬입니다. 국소성과 쌍곡성은 보존됩니다(5절 참조).
2.3 콤팩트 연산자 아인슈타인 유사 방정식
물질/필드 기여도를 연산자 스트레스 텐서 𝑇̂μν로 수집하고 Ψ로 투영하면
Gμν[g] = <Ψ|𝑇̂μν[M, g, A, Φ]|Ψ> - ½ (∇μ∇ν - gμν□) ln F(I, K, Γ). (12)
이것은 프레임워크의 핵심에 있는 콤팩트 방정식입니다. 국소 등각 구동기, 정보 드라이버 및 연산자 값 물질 투영에 의한 GR 변형입니다.
2.4 (3, 2, 1)의 중앙화 장치에서 SM 출현
M(x) = diag(M3(x), M2(x), M1(x)), dim M3 = 3, dim M2 = 2, dim M1 = 1이라고 합시다. (13)
그러면 g = {X : [X, M] = 0} ≅ su(3) ⊕ su(2) ⊕ u(1). (14)
그리고 M과 가환하는 작은 게이지 요동은 정확히 SM 게이지 대수를 형성합니다. M-섹터에서 이차 요동 헤세 행렬은 운동 에너지 정규화를 결정합니다.
1/ga² ~ Hessian(LM)|block a ~~ 임계값을 갖는 SM 유사 실행. (15)
3 사고 실험: 확장된 서사적 기반
이 섹션에서는 수학으로 이어진 (그리고 일관성이 있는) 경험적이고 직관적인 비계를 제시합니다. 산문은 내 언어로 되어 있으며, 이제 명확성을 위해 정리되었고, 각 아이디어는 서사적 호를 깨지 않고 개념을 선명하게 하는 경우에만 공식으로 동반됩니다.
3.1 힐베르트 원 및 근접 타격

모든 국소 상태가 기하학적 기준선에 대해 위상이 맞춰진 각도 s를 인코딩하는 힐베르트 원을 전달한다고 상상해 보십시오. 원은 속임수가 아닙니다. 그것은 기하학에 중요한 특수 방향으로 상태가 기울 때 추적하는 가장 깨끗한 방법입니다. s = ±½에서 구별되는 반 상태와 s = ±1에서 기수 상태가 있습니다.

상태 각도가 이러한 위치를 스위핑하면 근접 타격의 가능성이 높아집니다. 근접 타격은 시공간을 전혀 발로 차지 않습니다. 충분한 탭이 조정된 창과 국소 곡률 메아리에서 드럼을 부드럽게 두드립니다. 이것은 비국소 마법이 아닙니다. 탭은 국소적이고, 스칼라적이며, 스칼라 포텐셜 ln F에서 작용하는 엄격하게 국소적인 미분 연산자를 통해 축적됩니다.
수학적으로 근접 타격 밀도는 다음과 같습니다.
K(x) = ∫ds w(s) <Ψ(x,s)|K̂(s)|Ψ(x,s)>,
-1
w(s)가 반 상태와 기수 점 근처에서 상승합니다. 실제적인 결론은 K가 해당 각도 근처에서 링클될 때 상승한다는 것입니다. 그러면 K는 F(I, K, Γ) 내부에 나타나고 연산자 ½ (∇μ∇ν - gμν□)가 국소적으로 작용하여 곡률을 공급합니다. 더 빠른 빛 지름길을 위한 공간은 없습니다. 드럼 치는 소리가 발 바로 아래에 있습니다.
3.2 강화 및 동기화
이제 느슨하게 결합된 많은 힐베르트 원의 그림을 그려보세요. 위상이 정렬되기 시작하면 완벽하지는 않지만 근접 타격이 더 조밀한 팩으로 도착하기 시작합니다. 저는 이것을 강화라고 부릅니다. 시스템은 전체 우주를 잠그려고 공모하지 않습니다. 천천히 진화하는 필드(여기서는 Γ로 캡처됨)가 각도를 공유된 홈으로 찌르는 것만으로 국소적으로 동기화됩니다.
매우 간단한 역학은 풍미를 포착합니다.
ττ ∂τΓ(x) = -Γ(x) + βK(x), 0 < β ≪ 1,
로컬로
ln F ≈ αI I(E) + αK K + αΓ Γ.
강화가 K와 Γ를 들어 올리면 곡률 드럼이 더 바쁜 탭 시퀀스를 얻습니다. 그런 다음 각도가 멀어짐에 따라 진정됩니다.
3.3 빅뱅 추력(전/후 빅뱅 전환)

세 개의 주요 힐베르트 원이 강력하게 정렬된 원시 이웃의 그림을 그려보세요.

이 소설을 지나치게 설명할 필요는 없습니다. 힐베르트 원이 나중에보다 훨씬 더 일반적이었던 시대일 뿐입니다. 근접 타격의 급증은 등각 연산자를 통해 실행되어 팽창인 빅뱅 추력을 밀어냅니다. 동기화가 해체될 때까지요.

추력을 지나면 고전적인 팽창 규칙이 적용되고 현재 관찰자는 추력이 설정하는 데 도움이 된 광범위한 필드에서 이국적인 것을 보지 못합니다.

제가 때때로 그 정렬된 사전 빅뱅 상태에 사용하는 별명은 Soup In A Clock입니다. 그것은 여기에 있고 이 논문의 다른 곳에는 없습니다. 이 수학은 브랜드가 필요하지 않습니다. 국소성과 쌍곡성이 손상되지 않은 '짧은 창'에만 필요합니다.

3.4 규모 의존적 관찰
전자 크기의 관찰자는 우리가 하는 것과 동일한 힐베르트 원 스윕을 경험하지 않습니다. 해당 규모에서는 빠른 회전이 백그라운드 비트입니다. 경험은 꾸준한 양입니다. 인간의 눈은 다른 비트를 봅니다.

동일한 국소 물리학, 동일한 원, 시계는 다른 규모로 다르게 작동합니다. 속임수가 아닙니다. 명백한 것을 명시하는 것입니다. 자신의 메트로놈으로 템포를 판단합니다.
3.5 국소성 보존
이 프레임워크의 모든 부분은 빛보다 빠르게 달리는 것이 없도록 구축되었습니다. 등각 구동기는 주요 부분이 파 연산자의 주요 부분과 일치하는 미분 연산자로 처리됩니다. 선형화(아래)는 원뿔이 인과 관계를 유지함을 보여줍니다. 드럼 소리를 들을 수 있다면 바로 옆에 서 있기 때문입니다.
4. 기능적 정보: 에너지 연결, 로그 불변 드라이버
4.1 정의 및 근거
우리는 다음을 정의합니다.
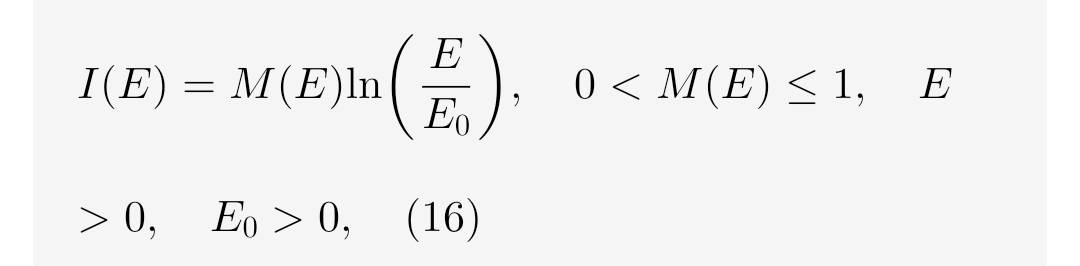
I(E) = M(E) ln(E/E₀), 0 < M(E) ≤ 1, E > 0, E₀ > 0, (16)
의미는 다음과 같습니다.
- E는 구성과 관련된 국소 에너지(또는 에너지 밀도)입니다.
- E₀는 무차원 로그 인수를 보장하고 I(E₀) = 0을 설정하는 고정된 기준 에너지입니다.
- *M(E)*는 사용 가능하거나 접근 가능한 구성을 가중합니다. 상수 또는 에너지에 따라 달라질 수 있습니다.

로그는 상대적 변화를 캡처합니다(에너지를 두 배로 늘리면 기준에 관계없이 I에 상수가 추가됨). 심층 정보 이론 및 열역학적 패턴과 일치합니다. Linfo에서

Linfo = αI I(E) + αK ∫ds (<Ψ|K̂(s)|Ψ>),
스칼라 ln *F(I, K, Γ)*는 국소 2차 등각 연산자를 통해 메트릭 방정식에 나타납니다. 이것이 기능적 정보가 곡률 드럼을 탭하는 방법입니다.
4.2 기본 속성
보조 정리 4.1(단조성 및 정규화). *M(E)*가 감소하지 않고 E₀ > 0이면 *I(E)*는 증가합니다. 단위를 변경하면 E가 재조정되지만 E₀에 의해 흡수되어 무차원 비율과 따라서 ln(E/E₀)가 보존됩니다.
보조 정리 4.2(변동 감도). δI/δE = M'(E) ln(E/E₀) + M(E)/E. 특히 M이 느리게 변하면 *δI/δE ≈ 1/E*이고, 에너지에 대한 등각 응답은 규모별 로그입니다.
5. 쌍곡성, 인과성 및 올바르게 구성된 IVP
5.1 선형화 및 주요 기호
대칭 2-텐서에 작용하는 □g의 기호와 일치하는 조화 게이지에서 (8)을 (ḡ, M̄, Ψ̄)에 대해 선형화합니다. 등각 수정은
δ[½ (∇μ∇ν - gμν□) ln F] = ½ (∇μ∇ν - ḡμν□) δ ln F + (낮은 차수),
주요 부분을 보존합니다. 따라서:
정리 5.1(국소 쌍곡성). 부드러운 배경과 허용 가능한 F > 0의 경우 선형화된 메트릭 방정식은 c로 제한된 인과 원뿔이 있는 쌍곡선입니다. 초기 값 문제는 표준 소볼레프 공간에서 국소적으로 올바르게 구성됩니다.
주석 5.1. 엄격한 국소성은 연산자 수준에서 인코딩됩니다. 등각 소스는 2차 공변 연산자로 처리되는 국소 스칼라입니다. 비국소 전파자는 없습니다. 이것은 국소성 보존을 명시적으로 실현합니다.
6. 요동의 양자화 (가우스 부문)
6.1 이차 확장
Φ가 (g, M, Ψ,...)의 요동을 수집하도록 합시다. 정지 솔루션에 대해 2차로 S를 확장하면 다음이 생성됩니다.
δ²S = ½ ∫ d⁴x √-ḡ δΦ D δΦ + ...,
여기서 D는 블록 미분 연산자입니다(메트릭에서는 파형, 다른 섹터에서는 타원 + 쌍곡선 혼합). 기능적 적분
Z ≈ ∫ [DΦ] exp(½δ²S)
는 가우스이며, D의 역수로 주어지는 2점 함수를 갖습니다. 이러한 전파기에 *K(x)*와 *I(E)*가 나타납니다.
6.2 2점 함수 및 연속체 스케일링
형식적으로는
<δΦ(x) δΦ(y)> ≈ i D⁻¹(x, y),
경계/게이지 조건은 일관되게 선택됩니다. 근접 타격 가중치 *w(s)*와 느린 강화 Γ는 쌍곡성을 깨지 않고 저주파 응답을 기울입니다.
7. RG 복도 및 임계값: SM 실행에 매핑
7.1 원 루프 실행
SM에서
μ dga/dμ = ba/16π² ga³, ba = (b3, b2, b1) = (-7, -19/6, 41/10),
그리고 αa = ga²/4π에 대해 동등하게:
μ dαa⁻¹/dμ = -ba/2π.
임계값은 M과 등각 구동기의 완화된 변형으로 구현됩니다. 임계값 규모에서 단계별 수정으로 나타나거나 유한 매칭으로 나타납니다.
7.2 복도 구성
명제 7.1(근사 통일 복도). 높은 에너지에서 공통 복도로 접근하는 αa⁻¹(μ)의 변형에 대한 공동 차원 1 패밀리(M, ln F) 변형이 존재하며, 5절의 헤세 행렬과 쌍곡성 제약 조건의 양성에 적용됩니다.
7.3 2루프 안정화(스케치)
2루프 기여는 경사를 개선하고 근사 복도를 안정화합니다. 운동 에너지 정규화가 M-섹터 헤세 행렬에서 발생하므로 임계값은 M 변형을 통해 스캔하여 자연스럽게 실행 가능한 커플링의 패밀리를 생성합니다.
8. 통계, 다른 곳에서 찾기 효과 및 절제
8.1 영역별 테스트
우리는 채널당 p-값을 계산하기 위해 영역별 배경 시험(위상/DM 스크램블, 템플릿 지터)을 강조합니다. 단일 이벤트 및 스택 통계(Stouffer Z 또는 Fisher 조합)와 LEE에 대한 Bonferroni 제어를 모두 보고합니다.
8.2 공동 유의성 및 상관 관계
pᵢ를 영역별 p-값이 Zᵢ = Φ⁻¹(1 - pᵢ)로 변환되도록 합시다. 상관 관계를 고려한 분모를 사용하는 Stouffer 방법:
Zjoint = (∑Zi) / (√∑ij ρij), ρij = {1 estimated cross-corr i ≠ j}.
이는 영역이 배경 모드를 공유할 때 낙관적인 인플레이션을 방지합니다.
8.3 절제 및 위조
두 가지 중요한 절제:
- ln F 드라이버에서 벗어나는 것 → 영역 간 적합도가 저하되고 근접 타격 예측력이 손실됩니다.
- scont(ℓ)(연속체 매핑)를 상수로 대체 → 스케일링이 일치하지 않고 RG 정렬이 약화됩니다.
실행 가능한 ToE 후보는 필수 부분을 제거하면 부드럽게 실패해야 합니다.
9. M-섹터에서 SM 운동학 유도
9.1 중앙화 장치 대수
M = diag(λ₃ 1₃, λ₂ 1₂, λ₁ 1₁)을 주요 순서로 작성합니다. 그런 다음 X는 X가 블록 대각선인 경우에만 M과 가환됩니다. 블록 Xᵢ ∈ u(3), X₂ ∈ u(2), X₁ ∈ u(1). 추적 중복성을 제거한 후에는
g ≅ su(3) ⊕ su(2) ⊕ u(1).
이 대수에서 m에 가환하는 Aμ의 작은 요동.
9.2 헤세 행렬 및 운동 에너지 정규화
배경 주위로 LM을 2차로 확장하면
δ²LM = ½ Tr((∇δM)ᵀ(∇δM)) - ½ δMV''(M)δM + ....
중앙화 장치로 요동을 투영하면 정규화가 1/ga²에 해당하는 운동 에너지 항이 생성됩니다. M의 부드러운 변형은 블록 구조에 정렬된 임계값 보정을 생성합니다. 이는 효과 필드 이론 언어에서 표준 매칭 절차에 매핑됩니다.
10. 분석과 에너지 추정치
10.1 주요 기호 및 게이지 고정
조화 게이지에서 선형화된 아인슈타인 연산자는 대칭 2-텐서와 낮은 차수 커플링에 대한 파 연산자입니다. 등각 항은 비앙키 항등식에 의해 전파된 제약 조건이 있는 메트릭 구성 요소에서 쌍곡선인 스칼라 2차 연산자를 제공합니다. 결합된 시스템(hμν, δM, δΨ)은 비앙키 항등식에 의해 전파되는 제약 조건이 있는 메트릭 구성 요소에서 쌍곡선을 유지합니다.
10.2 에너지 추정치
코시 슬라이스에서 (hμν, ∂t hμν)에 대한 표준 에너지 놈을 정의합니다. 국소 시간 내 추정치는 작음과 부드러움 가정 하에서 주요 기호의 강제력에서 비롯됩니다.
11. 기하학에서 신호로: 최소한의 교차 영역 맵
11.1 관찰 가능한 힐베르트 기하학
"기하학 대 신호" 노브(예: α, αK, scont(ℓ), 감쇠 법칙)의 작은 집합은 GW, 짧은 GRB, 저주파 AGN 방랑 및 좁은 PTA 잔차에 걸쳐 동일한 단순 신호 템플릿 패밀리를 각인하는 데 충분합니다. 모델의 간결성이 중요합니다. 몇 개의 노브, 많은 영역.
11.2 위조 가능한 제약 조건
- 근접 타격 급증 → 등각 구동에서 일관된 범프 → 영역 전체에서 일관된 관찰 가능한 각인.
- 블록 대각 M은 SM 대수를 강제 적용합니다. 편차는 구성되지 않은 혼돈이 아닌 임계값 변형에 영향을 미칩니다.
A. 표기법 및 규칙
시공간 지수 μ, ν = 0, 1, 2, 3; 메트릭 서명 (-, +, +, +). 힐베르트 각도 s ∈ [-1, 1]는 핵심 이론에서 연속적입니다. 내 규칙은 Δs = 0.1 증분으로 s를 이산화하는 것을 허용합니다. 근접 타격의 분석, 진단 및 이벤트 계산에 사용됩니다. 구별되는 반 상태 s = ±½ 및 기수 상태 s = ±1은 동적으로 두드러집니다.
감사
이 일반 이론에 큰 영향을 준 통찰력을 가진 커뮤니티의 공개 데이터 세트(중력파 공개 과학, FRB 공개 카탈로그)와 기본 토대를 마련한 거인들에게 감사합니다.
참고 문헌
[1] A. Einstein, "Die Feldgleichungen der Gravitation", Sitzungsberichte der Preußischen Akademie der Wissenschaften zu Berlin, 1915.
[2] A. Einstein, "Die Grundlage der allgemeinen Relativitätstheorie", Annalen der Physik, 1916.
[3] D. Hilbert, "Die Grundlagen der Physik", Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 1915.
[4] M. Planck, "On the Law of Distribution of Energy in the Normal Spectrum", Annalen der Physik, 1901.
[5] E. Schrödinger, "An Undulatory Theory of the Mechanics of Atoms and Molecules", Phys. Rev., 1926.
[6] P. A. M. Dirac, "The Quantum Theory of the Electron", Proc. Roy. Soc. A, 1928.
[7] J. von Neumann, Mathematical Foundations of Quantum Mechanics, 1932.
[8] S. W. Hawking, "Particle Creation by Black Holes," Commun. Math. Phys., 1975.
[9] L. Susskind, "The World as a Hologram," J. Math. Phys., 1995.
[10] R. Penrose, The Road to Reality, 2004.
[11] J. W. Szostak, "Functional information: Molecular messages," 2003.
[12] M. Wong and H. Hazen, "Functional Information in Physical Systems," 2023.
[13] LIGO/Virgo/KAGRA Collaboration, "Gravitational-Wave Open Science Center (GWOSC)," https://www.gw-openscience.org/.
[14] CHIME/FRB Collaboration, "Public Catalogs and Documentation," https://www.chime-frb.ca/.
chime-frb-web
www.chime-frb.ca
작업중...
