포논 (Phonons)

포논 (Phonons)

한글판 :
https://www.dola.com/thread/a5d4ef199a0ae

포논 - Dola

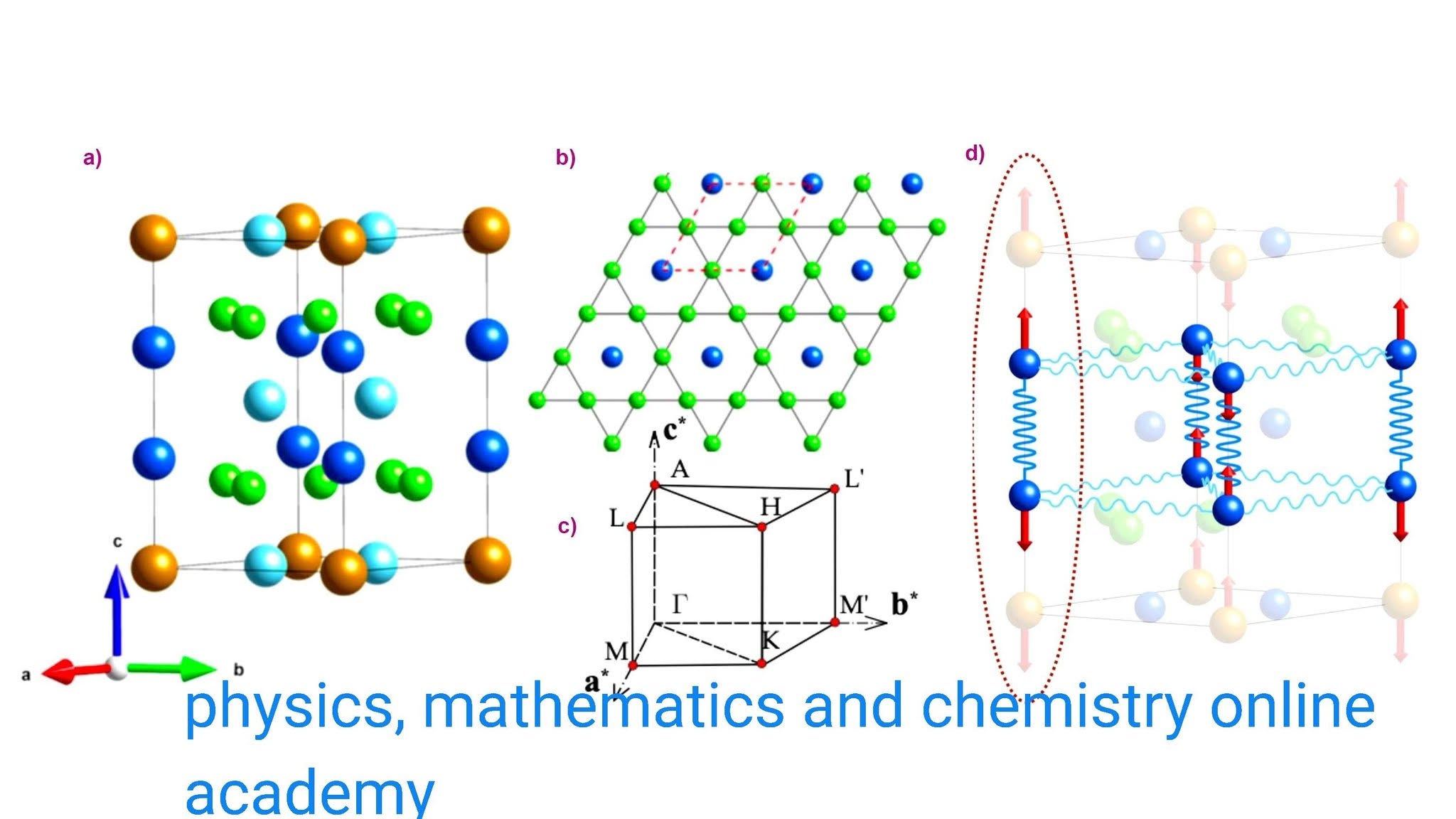
Phonons
➡️Introduction:
Phonons are quantized modes of vibrations in a crystal lattice, which can be thought of as particles that carry energy and momentum. They are the quanta of sound waves in a solid, similar to photons being the quanta of light.

➡️Properties of Phonons
1. Quasi-particles:
Phonons are not real particles, but rather a way to describe the collective behavior of atoms in a crystal lattice.
2. Bosons:
Phonons obey Bose-Einstein statistics, which means they can occupy the same quantum state.
3. Energy:
Phonons have energy E = ħω, where ω is the angular frequency of the vibration.
4. Momentum: Phonons have momentum p = ħk, k is the wavevector.

➡️Types of Phonons
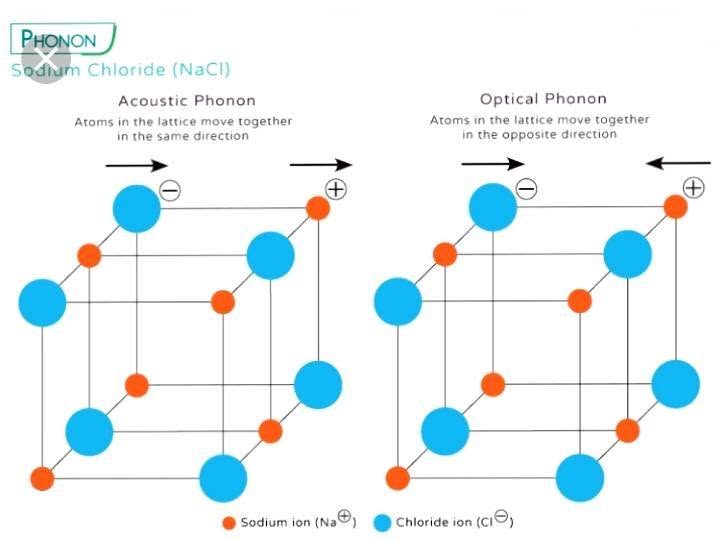
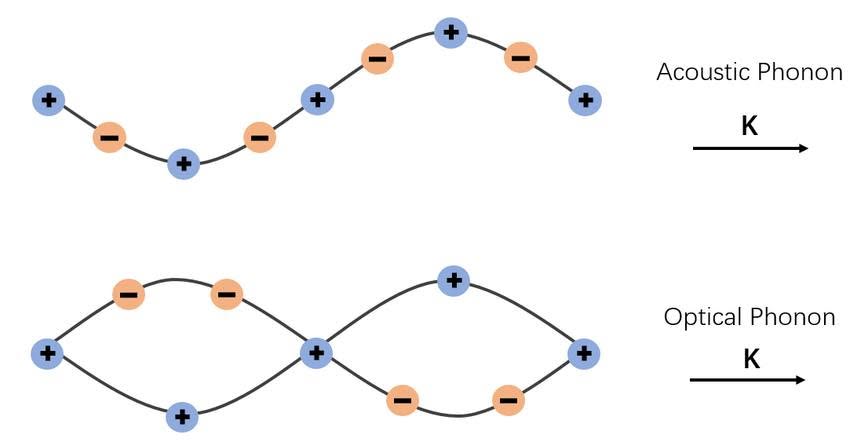
1. Acoustic Phonons:
Low-energy phonons with a linear dispersion relation (ω = vk), where v is the speed of sound.
2. Optical Phonons:
High-energy phonons with a non-linear dispersion relation, typically involving the vibration of atoms against each other.

➡️Phonon Dispersion Relations
The phonon dispersion relation describes the energy of phonons as a function of their wavevector. It can be calculated using lattice dynamics or measured experimentally using techniques like inelastic neutron scattering.

The dispersion relation for a one-dimensional monatomic lattice is given by:

ω(k) = √(4K/M) |sin(ka/2)|

where K is the spring constant, M is the mass of the atom, and a is the lattice constant.

For a three-dimensional lattice, the dispersion relation is more complex and depends on the crystal structure and interatomic forces.

➡️Importance of Phonons
1. Thermal Conductivity:
Phonons are responsible for heat transport in insulators and semiconductors.
2. Specific Heat:
Phonons contribute to the specific heat capacity of solids.
3. Superconductivity:
Phonons play a crucial role in the BCS theory of superconductivity.
4. Thermal Expansion:
Phonons are responsible for the thermal expansion of solids.

➡️Phonon Scattering Mechanisms
Phonons can be scattered by various mechanisms, including:

1. Phonon-Phonon Scattering: Phonons can interact with each other, leading to scattering and thermal resistance.
2. Phonon-Impurity Scattering:
Phonons can be scattered by impurities or defects in the lattice.
3. Phonon-Electron Scattering: Phonons can interact with electrons, leading to scattering and energy transfer.

➡️Experimental Techniques
1. Inelastic Neutron Scattering: Measures the phonon dispersion relation and density of states.
2. Raman Spectroscopy: Measures the phonon frequencies and linewidths.
3. Infrared Spectroscopy: Measures the phonon frequencies and absorption spectra.

➡️Examples
1. Diamond: Diamond has a very high thermal conductivity due to its stiff lattice and high phonon velocities.
2. Silicon: Silicon has a relatively high thermal conductivity, making it useful for electronic applications.

➡️Mathematical Formulation
The phonon Hamiltonian can be written as:

H = ∑(p^2/2M + (1/2)Mω^2u^2)

where p is the momentum, u is the displacement, and ω is the frequency.

Using the harmonic approximation, the phonon dispersion relation can be calculated by diagonalizing the dynamical matrix:

D(k) = ∑(K/R)e^(ikR)

where K is the spring constant, R is the lattice vector, and k is the wavevector.

The phonon frequencies and eigenvectors can be obtained by solving the eigenvalue equation:

D(k)e(k) = ω^2(k)e(k)

where e(k) is the eigenvector and ω(k) is the frequency.