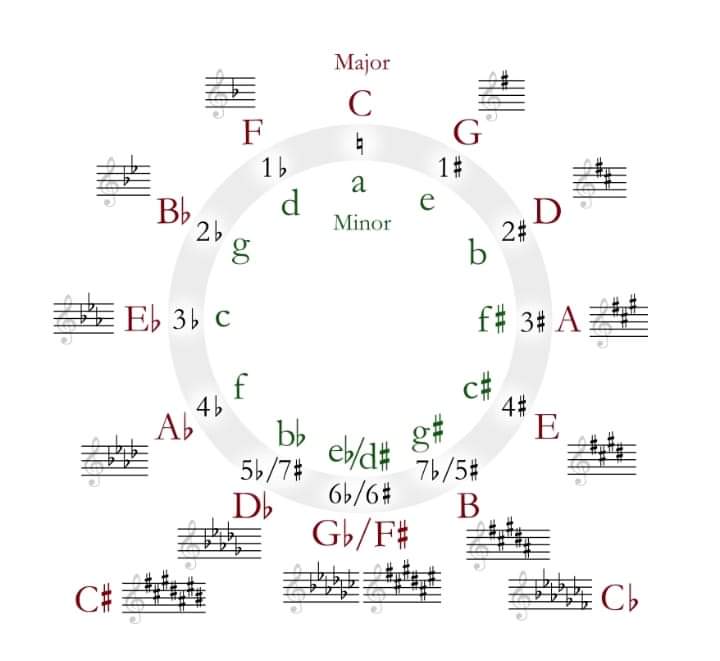
음계 5도의 원
음악 이론에서 5도권은 12개의 반음계를 완전 5도의 시퀀스로 구성하는 방법입니다. (이것은 표준 12음 동음 평균율 시스템에서 엄격히 적용됩니다.
다른 시스템을 사용하려면 감6도 음정 하나가 5도로 처리되어야 합니다.)
C를 시작점으로 선택한 경우 순서는 C, G, D, A, E, B(=C♭), F♯(=G♭), C♯(=D♭), A♭, E입니다. ♭, B♭, F. F부터 패턴을 계속하면 시퀀스가 시작점 C로 돌아갑니다.
이 순서는 가장 밀접하게 관련된 조표를 서로 인접하게 배치합니다. 일반적으로 원 형태로 표현됩니다.
5도 원은 완전 5도의 순서로 음정을 구성하며 일반적으로 음정(및 해당 키)이 시계 방향으로 진행되는 원으로 표시됩니다. 원은 종종 시계 반대 방향으로 사용되므로 4등분의 원이 됩니다.
서양 음악의 화성 진행은 일반적으로 작곡 내에서 이 시스템의 인접 키를 사용하므로 음악 작곡과 화성에 유용한 참고 자료가 됩니다.[1]
완전 5도는 단순 억양 체계를 사용하여 주파수 비율이 3:2인 두 음정으로 구성되지만, 이런 방식으로 12개의 연속 완전 5도를 생성한다고 해서 시작 음의 음고 클래스로 돌아가는 것은 아닙니다. 이를 조정하기 위해 악기는 일반적으로 동음 평균율 시스템으로 조율됩니다.
12개의 평균율 5도는 초기 음보다 정확히 7옥타브 높은 음으로 이어지며, 이로 인해 7개의 평균율 반음에 해당하는 완전 5도가 생성됩니다.
원의 상단에는 샤프나 플랫이 없는 C 메이저의 조가 표시됩니다. 시계방향으로 진행하면 음정이 5도씩 올라갑니다. 해당 음높이와 관련된 조표도 변경됩니다.
G 키에는 샤프가 1개 있고, D 키에는 샤프가 2개 있는 식입니다. 마찬가지로, 원의 위에서부터 시계 반대 방향으로 진행하면서 음표는 5도 내림차순으로 변경되고 이에 따라 조표도 변경됩니다.
즉, F 키에는 플랫이 1개 있고, B♭의 키에는 플랫이 2개 있는 식입니다. 원의 아래쪽에 있는 일부 키는 올림표나 올림표로 표기될 수 있습니다.
임의의 음조에서 시작하여 5도씩 오름차순으로 12개의 음을 모두 생성한 후 시작 음조 클래스로 돌아갑니다(음조 클래스는 옥타브에 관계없이 주어진 문자로 표시된 모든 음으로 구성됩니다.
예를 들어 모든 "C"는 동일한 피치( 클래스). 시계 반대 방향으로 이동하면 음조는 5도씩 내려가지만 완전 4도만큼 올라가면 같은 음이 한 옥타브 더 높아집니다(따라서 동일한 음조 (등급). C에서 시계 반대 방향으로 이동하는 것은 F로 5도 단위로 내려가거나 F로 4도 단위로 상승하는 것으로 생각할 수 있습니다.
다이아토닉 조표 (편집하다)
12개의 음정 각각은 장조 또는 단조의 강장제 역할을 할 수 있으며, 이러한 각 건반은 이와 관련된 온음계를 갖습니다. 원 다이어그램은 각 조표의 샤프 또는 플랫 수를 표시하며 장조는 대문자로 표시되고 단조는 소문자로 표시됩니다. 동일한 조표를 갖는 메이저 키와 마이너 키를 서로의 상대 메이저 및 상대 마이너라고 합니다.
변조 및 코드 진행 ( 편집하다)
음조 음악은 조표가 원본과 단 하나의 플랫 또는 샤프만 다른 새로운 음조 중심으로 변조되는 경우가 많습니다. 밀접하게 관련된 이러한 키는 서로 5분의 1 떨어져 있으므로 5분의 1 원 안에 인접해 있습니다. 코드 진행은 또한 근음이 완전 5도에 연결된 코드 사이에서 이동하는 경우가 많으므로 코드 사이의 "화음 거리"를 설명하는 데 5도의 원이 유용합니다.
5도권은 화음의 화성 또는 조성 기능을 구성하고 설명하는 데 사용됩니다.[2] 코드는 "기능적 연속"에서 오름차순 완전 4도(또는 하강 완전 5도라고도 함) 패턴으로 진행될 수 있습니다.
이는
"...5분의 1의 원으로 표시될 수 있습니다 (따라서 척도 차수 II가 척도 차수 IV보다 우세한 것에 더 가깝습니다)".[3]
이 관점에서 토닉 또는 토널 중심은 5도권에서 파생된 코드 진행의 끝점으로 간주됩니다.
동일하지 않은 튜닝 시스템의 원 폐쇄 (편집하다)
완전 5도(단지 억양)를 정의하기 위해 정확한 3:2 주파수 비율을 사용한다고 해서 5도 원을 돌고 난 후 시작 음의 피치 클래스로 돌아가는 결과가 나오지는 않습니다. 동음 평균율 튜닝은 초기 톤보다 정확히 7옥타브 위의 톤으로 돌아가는 5도를 생성하고 각 반음의 주파수 비율을 동일하게 만듭니다. 평균율 5도의 주파수 비율은 27/12:1(또는 약 1.498307077:1)이며, 비율이 3:2인 적절하게 조율된 5도보다 약 2센트 더 좁습니다.
적절하게 조율된 5도만큼 상승하면 약 23.46센트, 대략 반음의 1/4, 즉 피타고라스 쉼표로 알려진 간격을 초과하여 원을 닫는 데 실패합니다.
피타고라스 조율에서는 12도 중 하나의 폭을 현저히 줄여 심각한 불협화음을 만들어 이 문제를 해결합니다.
이 변칙적인 5번 째는 늑대 5번(Wolf Fifth)이라고 불리며, 이는 늑대가 음정을 벗어난 음을 울부짖는 것을 유머러스하게 언급한 것입니다. 1/4 쉼표 의미톤 튜닝 시스템은 동일한 단율의 5도보다 약간 좁은 11개의 5도를 사용하며 원을 닫으려면 훨씬 더 넓고 불협화음이 심한 울프 5도가 필요합니다. 5 제한 튜닝과 같은 단순한 억양을 기반으로 하는 더 복잡한 튜닝 시스템은 최대 8개의 정확하게 조율된 5도와 최소 3개의 비정 5도(일부는 5도보다 약간 좁고 일부는 약간 넓음)를 사용하여 원을 닫습니다.
다른 튜닝 시스템은 5도의 원을 닫기 위해 최대 53개 톤(원래 12개 톤과 그 사이에 42개 추가 톤)을 사용합니다.
Starting at any pitch and ascending by a fifth generates all twelve tones before returning to the beginning pitch class (a pitch class consists of all of the notes indicated by a given letter regardless of octave—all "C"s, for example, belong to the same pitch class). Moving counterclockwise, the pitches descend by a fifth, but ascending by a perfect fourth will lead to the same note an octave higher (therefore in the same pitch class). Moving counter-clockwise from C could be thought of as descending by a fifth to F, or ascending by a fourth to F.
Diatonic key signatures
edit
Each of the twelve pitches can serve as the tonic of a major or minor key, and each of these keys will have a diatonic scale associated with it. The circle diagram shows the number of sharps or flats in each key signature, with the major key indicated by a capital letter and the minor key indicated by a lower-case letter. Major and minor keys that have the same key signature are referred to as relative major and relative minor of one another.
Modulation and chord progression
edit
Tonal music often modulates to a new tonal center whose key signature differs from the original by only one flat or sharp. These closely-related keys are a fifth apart from each other and are therefore adjacent in the circle of fifths. Chord progressions also often move between chords whose roots are related by perfect fifth, making the circle of fifths useful in illustrating the "harmonic distance" between chords.
The circle of fifths is used to organize and describe the harmonic or tonal function of chords.[2] Chords can progress in a pattern of ascending perfect fourths (alternately viewed as descending perfect fifths) in "functional succession". This can be shown "...by the circle of fifths (in which, therefore, scale degree II is closer to the dominant than scale degree IV)".[3] In this view the tonic or tonal center is considered the end point of a chord progression derived from the circle of fifths.
Circle closure in non-equal tuning systems
edit
Using the exact 3:2 ratio of frequencies to define a perfect fifth (just intonation) does not quite result in a return to the pitch class of the starting note after going around the circle of fifths. Equal temperament tuning produces fifths that return to a tone exactly seven octaves above the initial tone and makes the frequency ratio of each half step the same. An equal-tempered fifth has a frequency ratio of 27/12:1 (or about 1.498307077:1), approximately two cents narrower than a justly tuned fifth at a ratio of 3:2.
Ascending by justly tuned fifths fails to close the circle by an excess of approximately 23.46 cents, roughly a quarter of a semitone, an interval known as the Pythagorean comma. In Pythagorean tuning, this problem is solved by markedly shortening the width of one of the twelve fifths, which makes it severely dissonant. This anomalous fifth is called the wolf fifth – a humorous reference to a wolf howling an off-pitch note. The quarter-comma meantone tuning system uses eleven fifths slightly narrower than the equally tempered fifth, and requires a much wider and even more dissonant wolf fifth to close the circle. More complex tuning systems based on just intonation, such as 5-limit tuning, use at most eight justly tuned fifths and at least three non-just fifths (some slightly narrower, and some slightly wider than the just fifth) to close the circle. Other tuning systems use up to 53 tones (the original 12 tones and 42 more between them) in order to close the circle of fifths