Differential calculus is a branch of mathematics that deals with changing quantities. It consists of two main concepts, **differentiation** and integration, and is closely related to each other. Simply put, differentiation is a tool for calculating instantaneous rates of change and integration is a tool for calculating accumulated quantities.
1. Differentiation:
- Concept: Differentiation is the process of finding the instantaneous rate of change of a function, that is, the slope. By calculating the slope of the tangent line at a specific point, it represents the rate of change of the function at that point. For example, the speed is the rate of change (differential) of the position, and the acceleration is the rate of change (differential) of the speed.
- Basic concept:
- Limit: The basis of differentiation is the concept of limit. It defines the instantaneous rate of change through the change in the function value for a very small amount of change.
- Derivative: The derivative result of a function is called a derivative. The derivative is another function that represents the slope of the original function.
- Differentiation rules: There are rules for easily calculating differentiation for various functions (e.g., differentiation of products, differentiation of synthetic functions, etc.).
- Use:
- Finding maximum/minimum: A point where the slope (derivative) of the function is 0 becomes an extreme (maximum or minimum) candidate.
- Finding the equation of the tangent line: The slope of the tangent line at a specific point can be obtained through the derivative.
- Applications in physics, engineering, etc.: used to calculate physical quantities such as speed, acceleration, curvature, etc.
2. Integration:
- Concept: Integration is the process of calculating the accumulated amount of a function. It is an inverse operation of differentiation, used to find the area (2 dimensions) or volume (3 dimensions) under the function.
- Basic concept:
- Indefinite integral: A function that differentiates to become the original function is called indefinite integral. It includes the integral constant C.
- Definite integral: The integral that calculates the area under the function in a specific interval.
- Integration techniques: There are techniques for easily calculating integrals for various functions (e.g., permutation integration, partial integration, etc.).
- Use:
- Area, volume calculation: Used to calculate the area surrounded by curves, volume of solids, etc.
- Calculation of mean values: Used to calculate the mean values of functions in a particular interval.
- Applications in physics, engineering, etc.: used to calculate physical quantities such as work, energy, mass, etc.
Relationship between differentiation and integration:
Differentiation and integration are in the relationship of inverse computation. Differentiating a function and then integrating gives the original function (integration constants must be considered). This relationship is known as the Fundamental Theorem of Calculus. This theorem serves as an important bridge between differentiation and integration and is used in many applications of calculus.
Summary:
Differential calculus is a powerful mathematical tool that deals with changing quantities. Differentiation calculates the instantaneous rate of change, integration calculates the accumulated amount, and is closely related to each other and applied to various fields. For more information, refer to the calculus textbook.
미분적분학은 변화하는 양을 다루는 수학의 한 분야입니다.
크게 **미분(微分, differentiation)**과 적분(積分, integration) 두 가지 주요 개념으로 구성되며, 서로 밀접하게 관련되어 있습니다.
쉽게 말해, 미분은 순간적인 변화율을, 적분은 누적된 양을 계산하는 도구입니다.
1. 미분 (Differentiation):
- 개념: 미분은 함수의 순간적인 변화율, 즉 기울기를 구하는 과정입니다. 특정 지점에서의 접선의 기울기를 계산하여, 그 지점에서의 함수의 변화 속도를 나타냅니다. 예를 들어, 속도는 위치의 변화율(미분)이고, 가속도는 속도의 변화율(미분)입니다.
- 기본 개념:
- 극한(Limit): 미분의 기본은 극한 개념입니다. 매우 작은 변화량에 대한 함숫값의 변화를 통해 순간적인 변화율을 정의합니다.
- 도함수(Derivative): 함수의 미분 결과를 도함수라고 합니다. 도함수는 원래 함수의 기울기를 나타내는 또 다른 함수입니다.
- 미분법(Differentiation rules): 다양한 함수에 대한 미분을 쉽게 계산하기 위한 규칙들(예: 곱의 미분법, 합성함수의 미분법 등)이 있습니다.
- 활용:
- 최대/최솟값 찾기: 함수의 기울기(도함수)가 0인 지점은 극값(최댓값 또는 최솟값) 후보가 됩니다.
- 접선의 방정식 구하기: 특정 지점에서의 접선의 기울기는 도함수를 통해 구할 수 있습니다.
- 물리학, 공학 등의 응용: 속도, 가속도, 곡률 등과 같은 물리량을 계산하는 데 사용됩니다.
2. 적분 (Integration):
- 개념: 적분은 함수의 누적된 양을 계산하는 과정입니다. 미분의 역연산으로, 함수 아래의 면적(2차원)이나 부피(3차원)를 구하는 데 사용됩니다.
- 기본 개념:
- 부정적분(Indefinite integral): 미분하면 원래 함수가 되는 함수를 부정적분이라고 합니다. 적분 상수 C를 포함합니다.
- 정적분(Definite integral): 특정 구간에서 함수 아래의 면적을 계산하는 적분입니다.
- 적분법(Integration techniques): 다양한 함수에 대한 적분을 쉽게 계산하기 위한 기법들(예: 치환적분, 부분적분 등)이 있습니다.
- 활용:
- 면적, 부피 계산: 곡선으로 둘러싸인 면적, 입체의 부피 등을 계산하는 데 사용됩니다.
- 평균값 계산: 특정 구간에서 함수의 평균값을 계산하는 데 사용됩니다.
- 물리학, 공학 등의 응용: 일, 에너지, 질량 등과 같은 물리량을 계산하는 데 사용됩니다.
미분과 적분의 관계:
미분과 적분은 역연산의 관계에 있습니다. 함수를 미분한 후 적분하면 원래 함수를 얻을 수 있습니다 (적분 상수를 고려해야 합니다). 이러한 관계는 미적분의 기본 정리로 알려져 있습니다. 이 정리는 미분과 적분을 연결하는 중요한 다리 역할을 하며, 미적분학의 많은 응용 분야에서 활용됩니다.
요약:
미분적분학은 변화하는 양을 다루는 강력한 수학적 도구입니다. 미분은 순간적인 변화율을, 적분은 누적된 양을 계산하며, 서로 밀접하게 연관되어 다양한 분야에 응용됩니다. 더 자세한 내용은 미적분학 교재를 참고하시면 좋습니다.



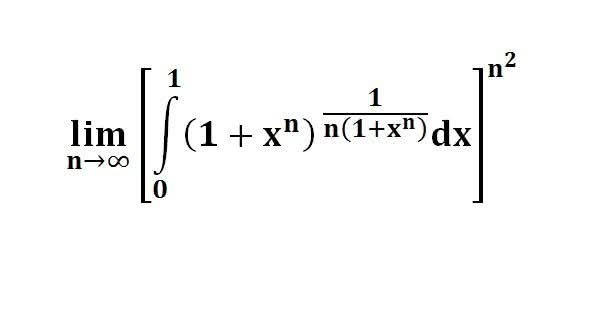
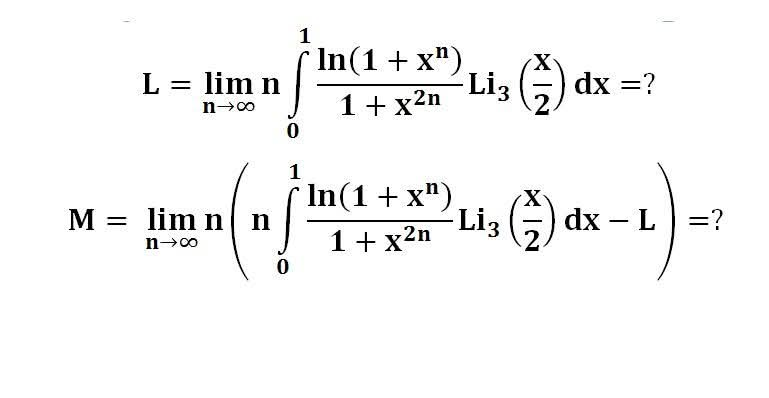
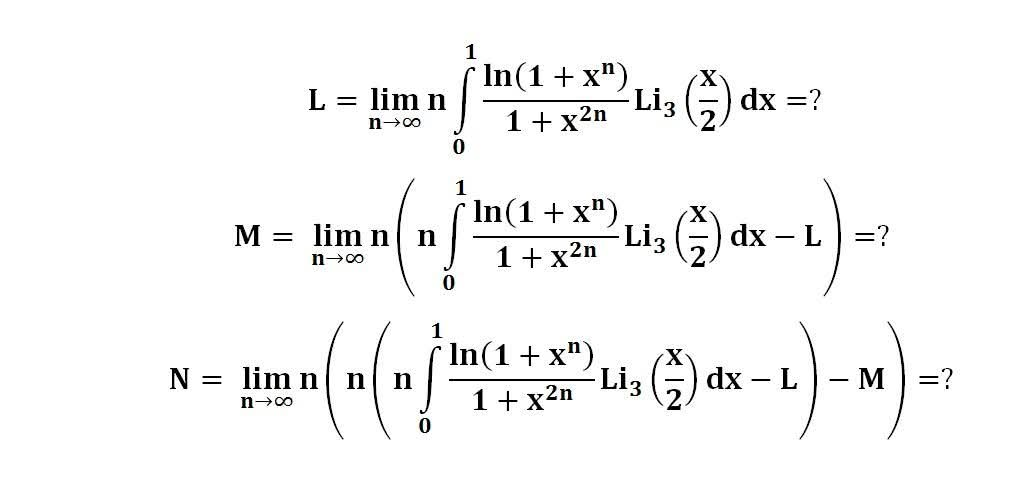
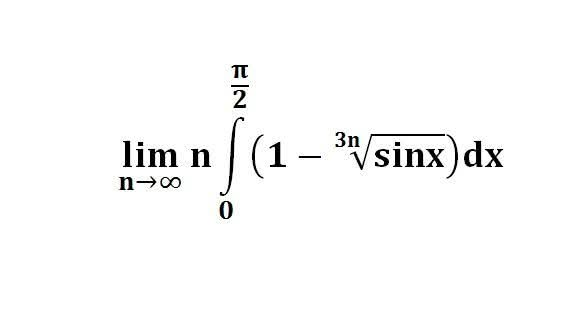
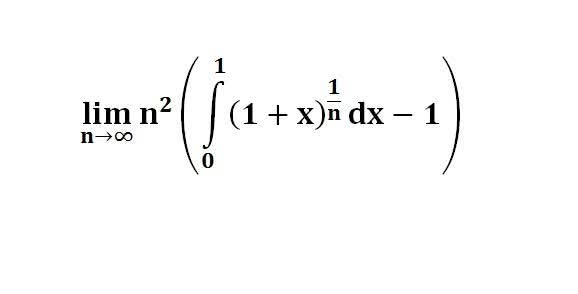
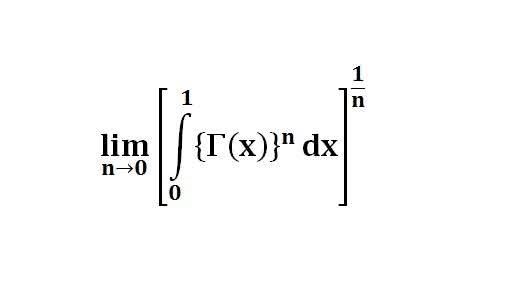
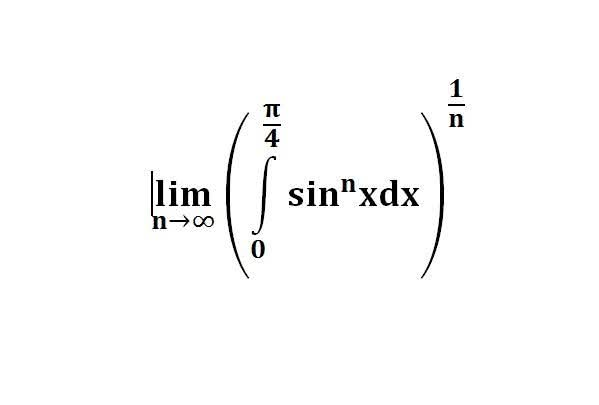
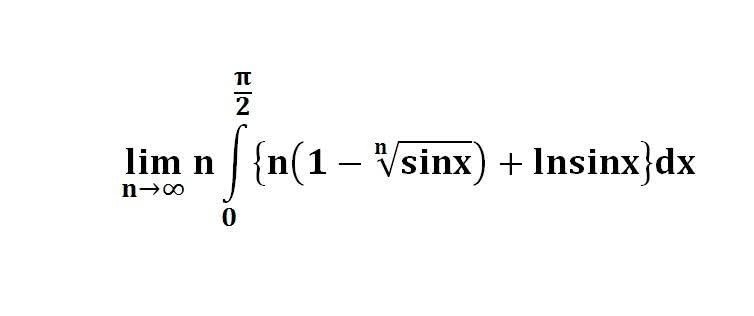
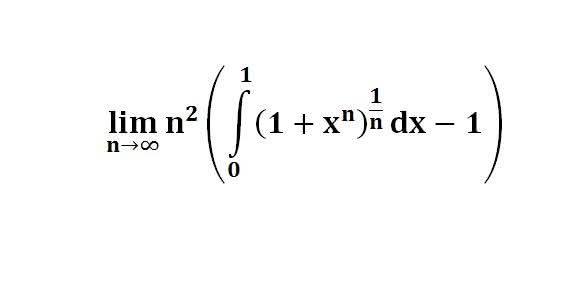
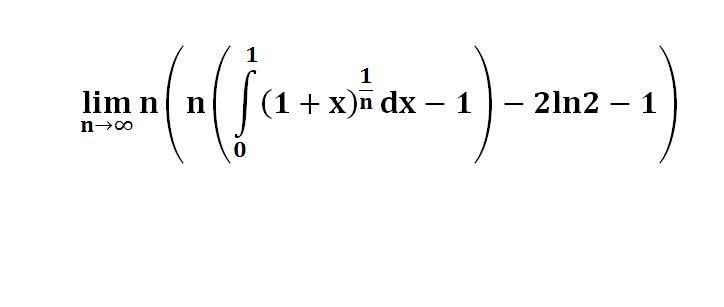
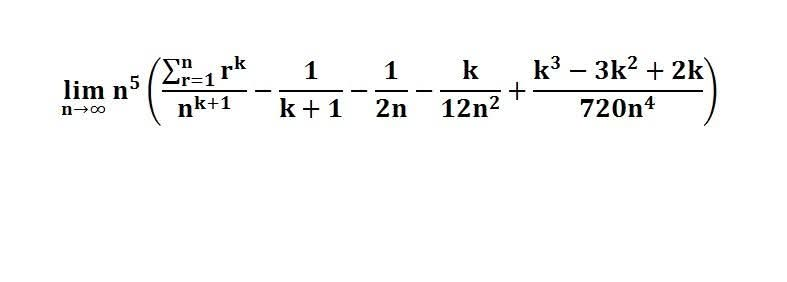
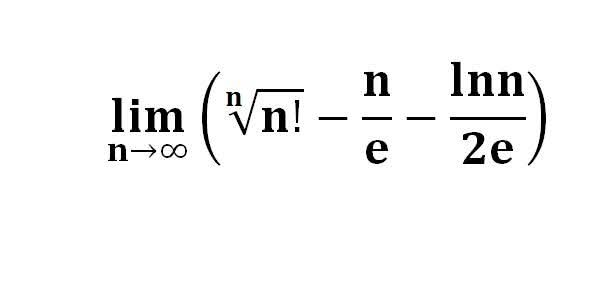
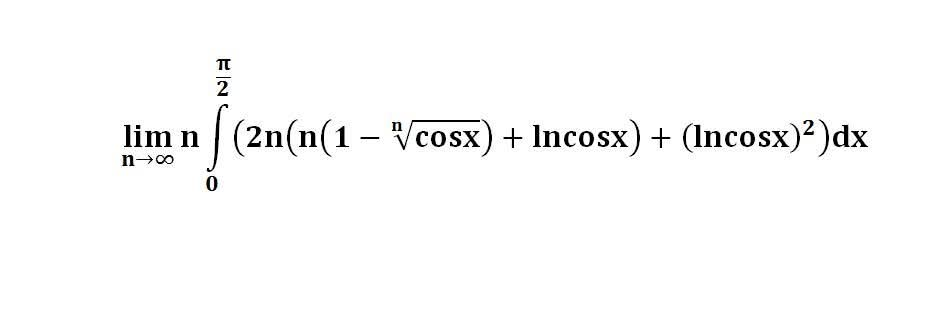
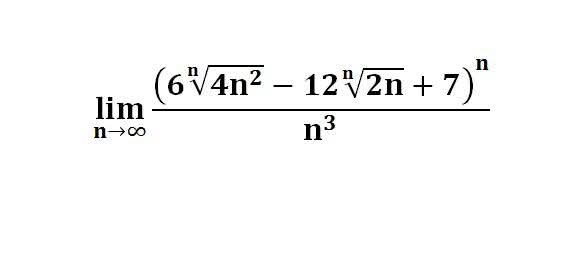
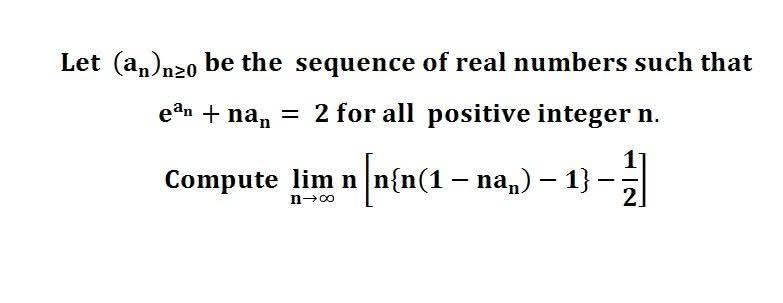
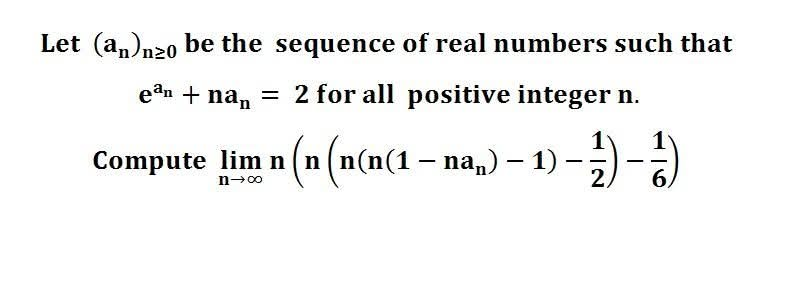

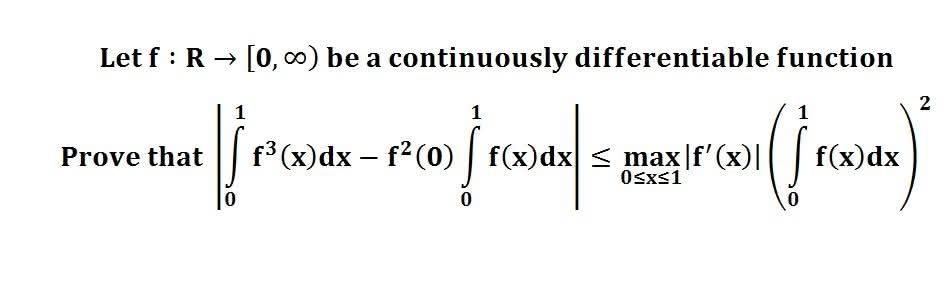
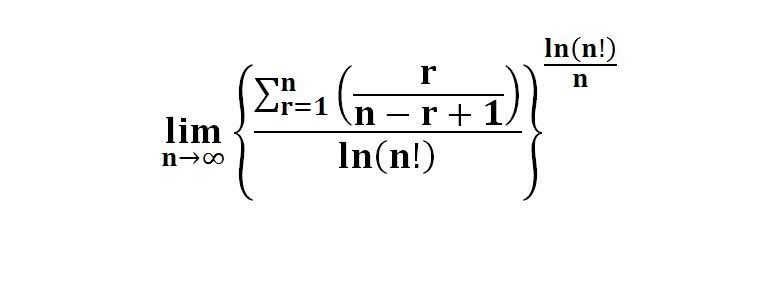
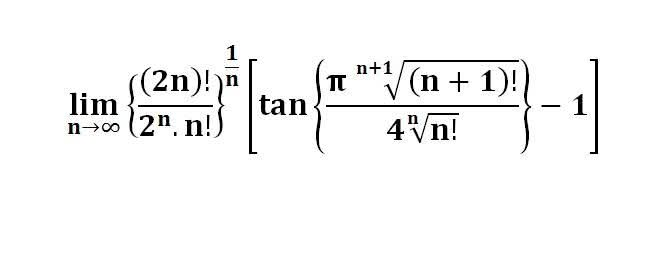
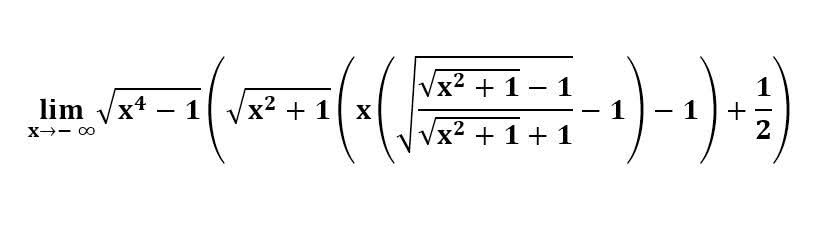
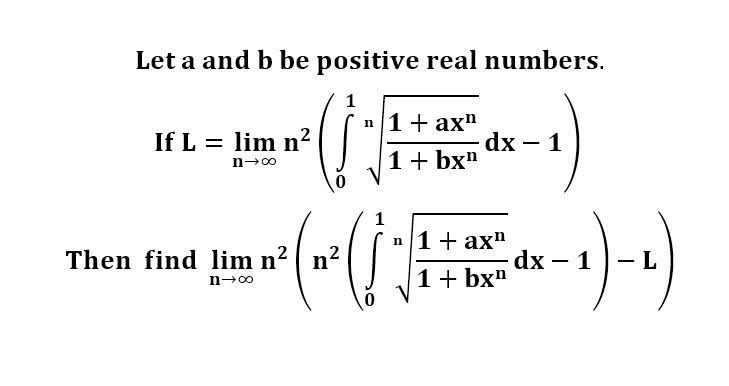
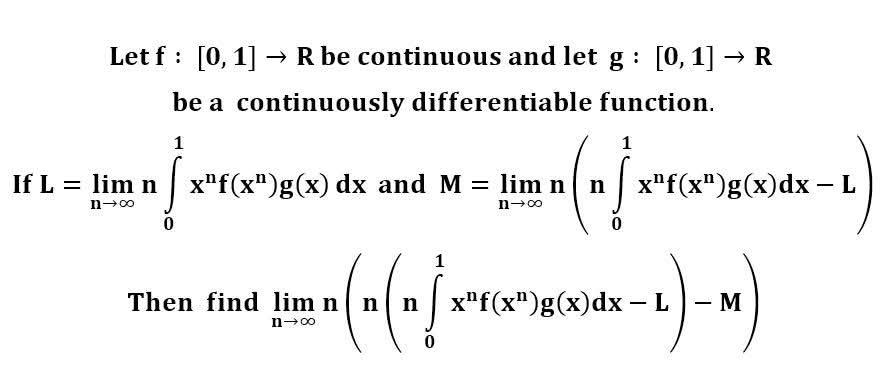
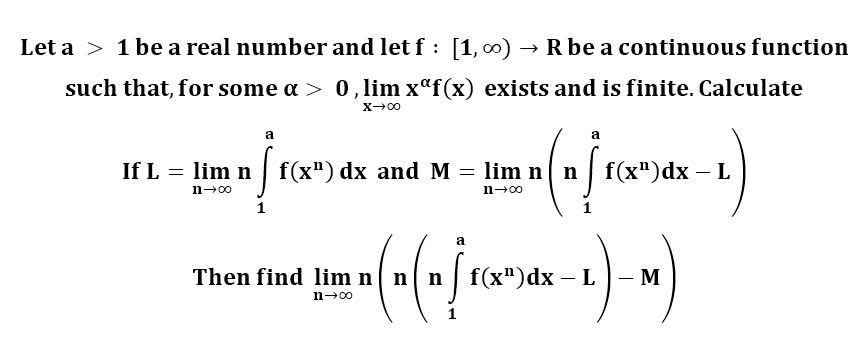

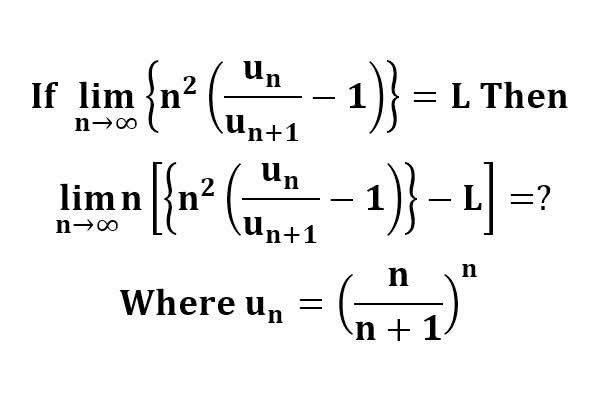
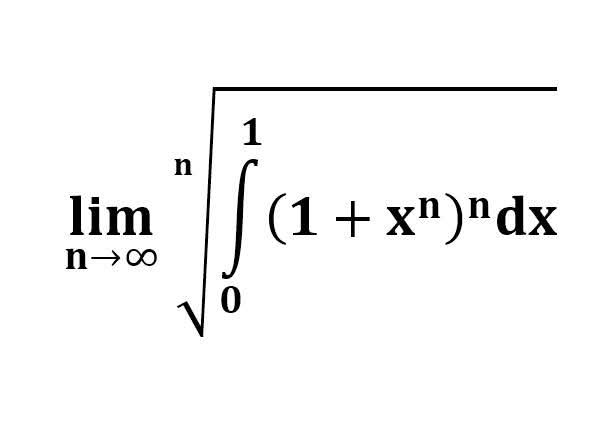
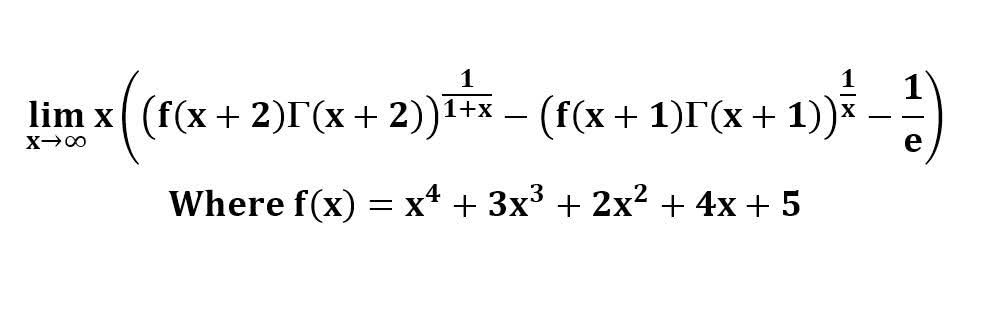
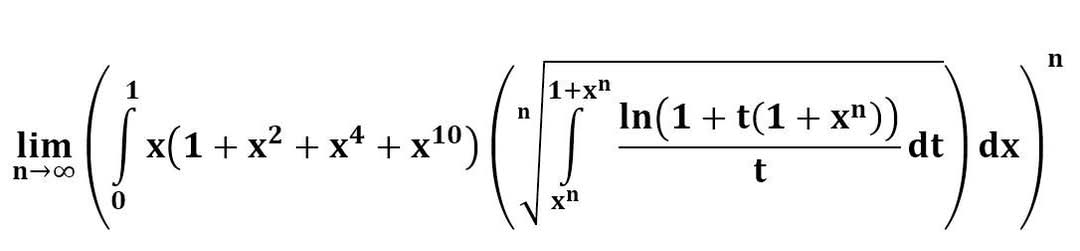
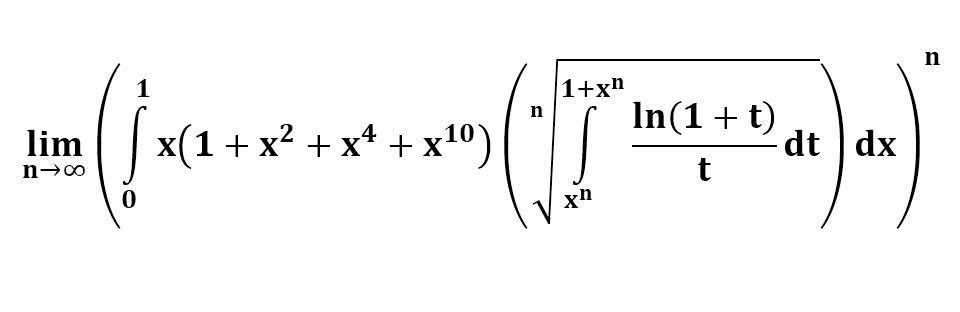
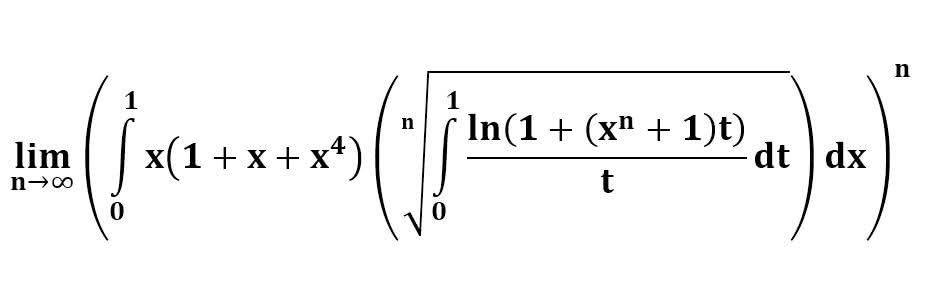
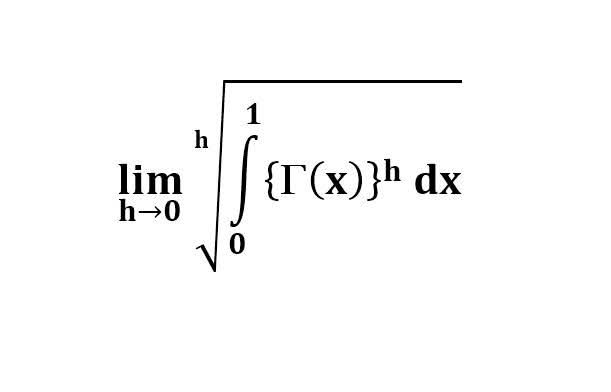
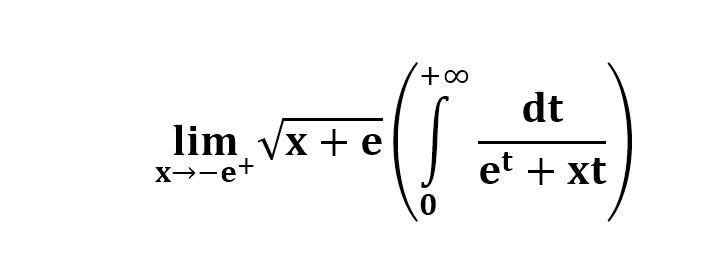
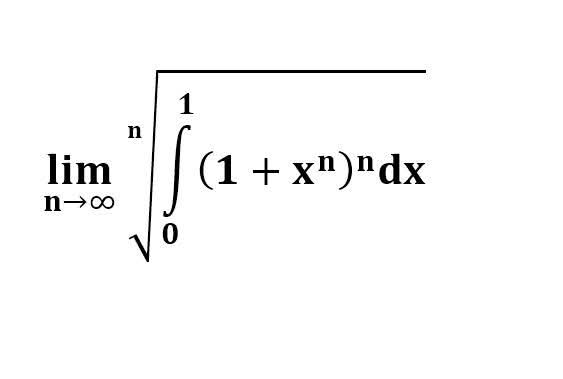
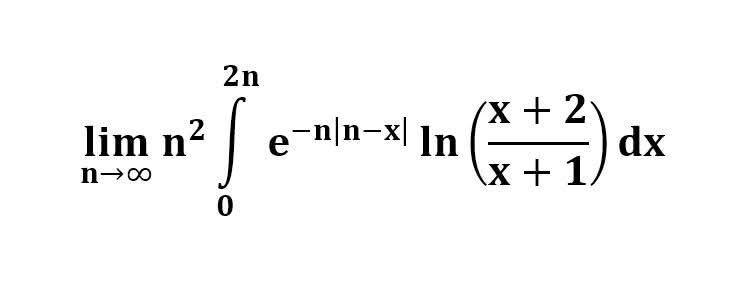
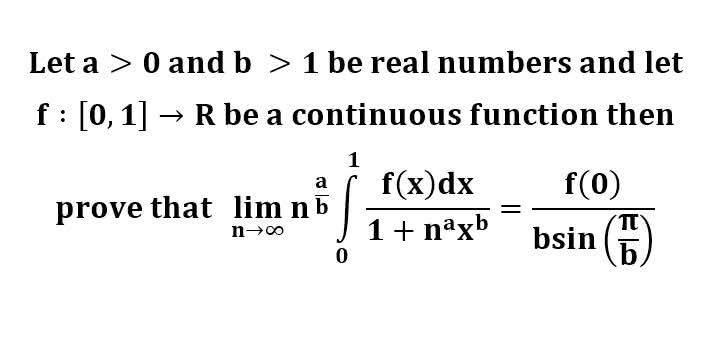

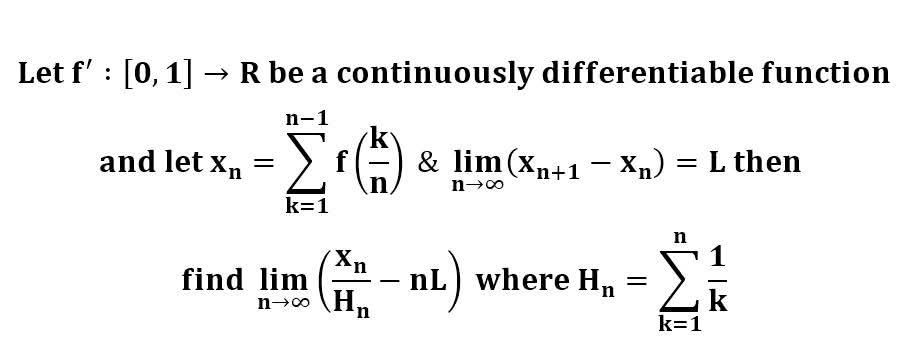

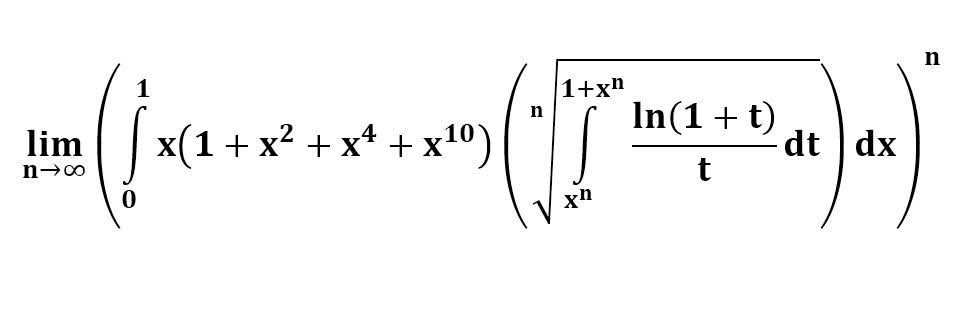
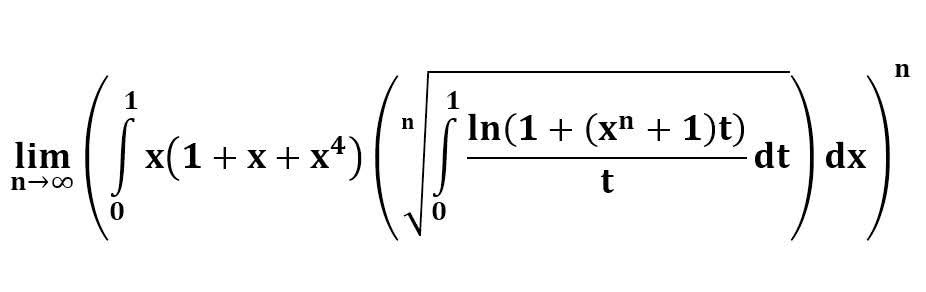
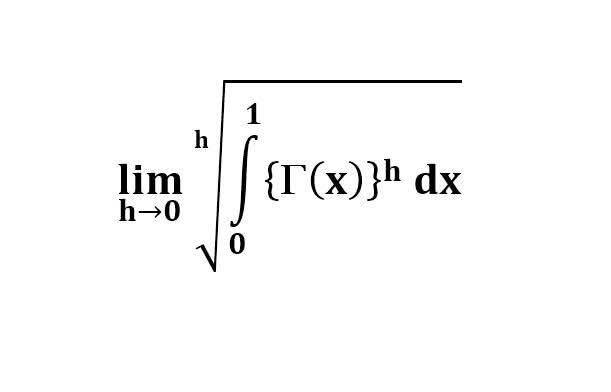
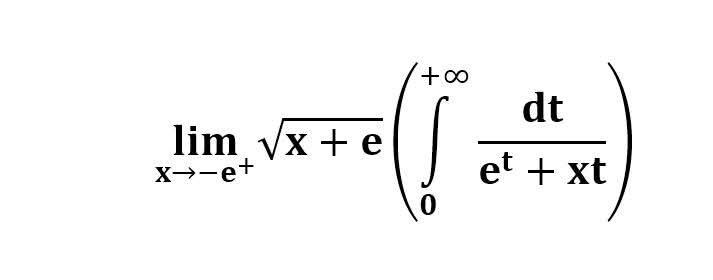
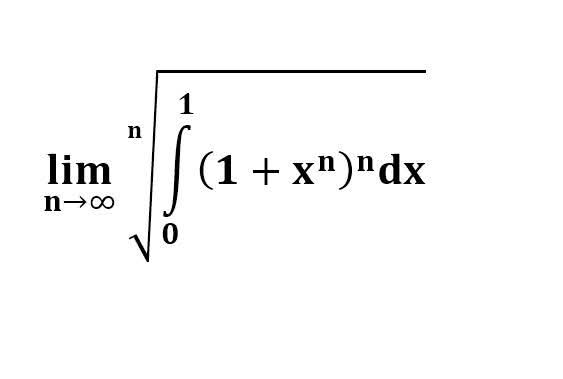
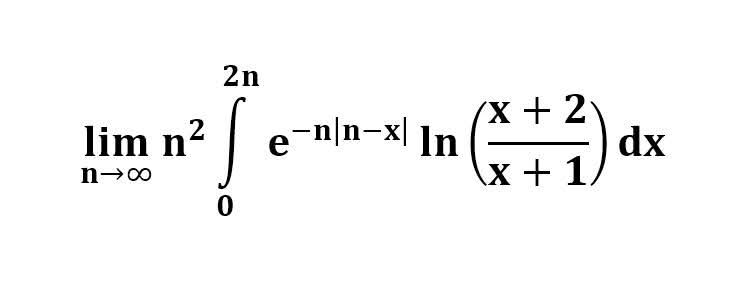
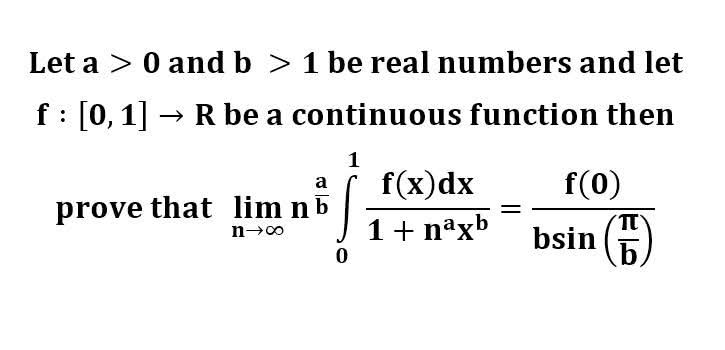

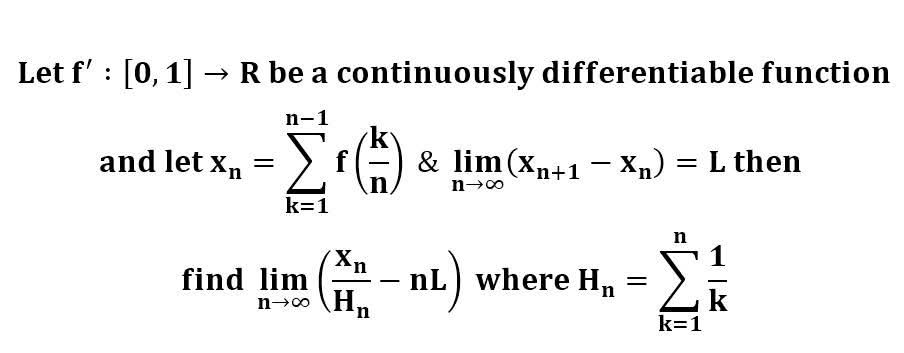


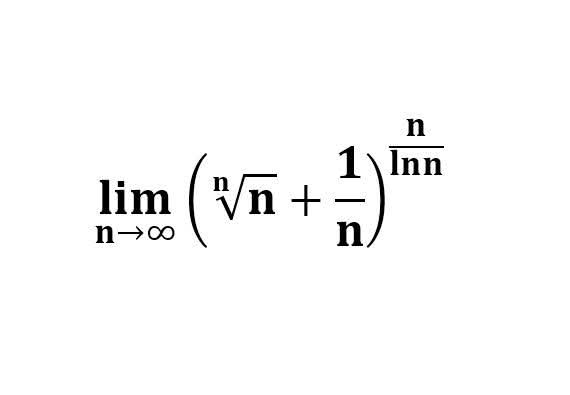


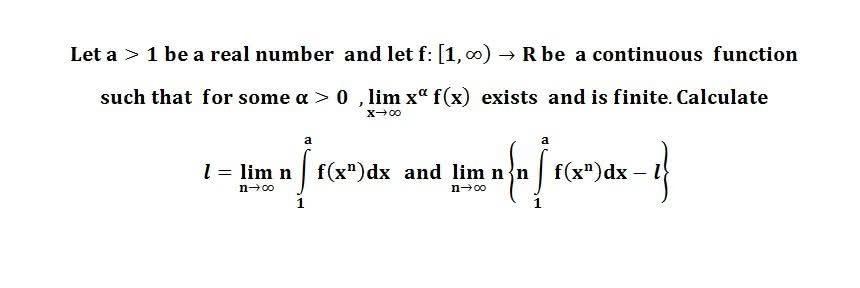
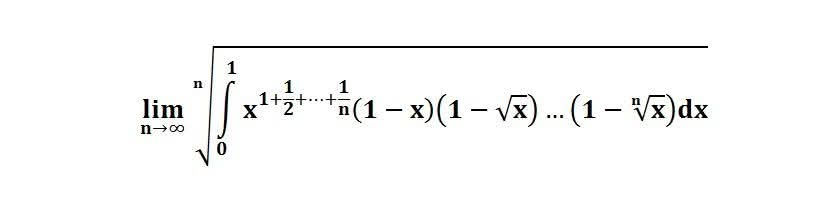


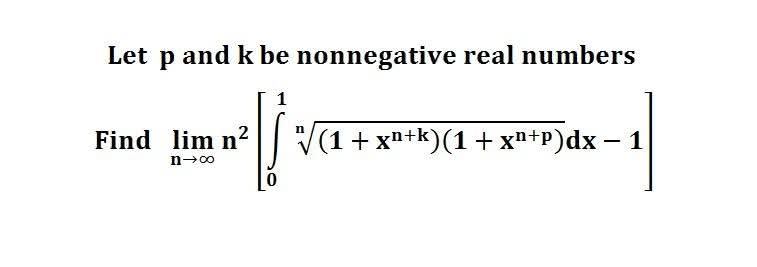
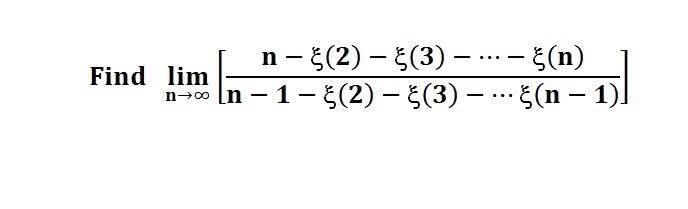
다음 수식의 해를 구하는 과정을 보여주세요.(AI설명)

풀이
이 문제는 극한과 적분을 포함하고 있으며, n이 무한대로 갈 때 피적분 함수의 행동을 이해하는 데 달려 있습니다.
1단계: 주어진 정보 이해
f: [0, 1] → ℝ이 연속 함수이고 g: [0, 1] → ℝ이 연속적으로 미분 가능한 함수라는 것을 알고 있습니다. 다음과 같이 주어집니다.
L = \lim_{n \to \infty} n \int_0^1 x^n f(x^n) g(x) dx
M = \lim_{n \to \infty} n \left( n \int_0^1 x^n f(x^n) g(x) dx - L \right)
다음을 구해야 합니다.
\lim_{n \to \infty} n \left( n \left( n \int_0^1 x^n f(x^n) g(x) dx \right) - L - M \right)
2단계: 피적분 함수 분석
핵심은 n이 매우 커짐에 따라 피적분 함수 x^n f(x^n) g(x)의 행동을 이해하는 것입니다. n → ∞로 가면, 0 ≤ x < 1에 대해 *xn*은 0으로 수렴하고 x = 1에 대해 1로 수렴합니다. 이 때문에 적분에 대한 주요 기여는 x가 1에 가까운 값에서 나올 것입니다.
치환을 해 보겠습니다. u = *xn*이라고 하면 x = *u1/n*이고 dx = (1/n) *u(1/n)-1 du가 됩니다. x = 0이면 u = 0이고, x = 1이면 u = 1입니다. 적분은 다음과 같이 됩니다.
n \int_0^1 u f(u) g(u^{1/n}) \frac{1}{n} u^{\frac{1}{n}-1} du = \int_0^1 u^{\frac{1}{n}} f(u) g(u^{1/n}) du
n→∞로 가면, u1/n → 1이고 g(u1/n) → *g(1)*이므로 적분은 다음과 같이 수렴합니다.
\int_0^1 f(u) g(1) du = g(1) \int_0^1 f(u) du
따라서 L은 g(1) ∫01 f(x) dx와 관련이 있을 가능성이 높습니다. 그러나 엄밀한 증명은 분석에서 더 고급 기술(아마도 지배 수렴 정리 포함)을 요구합니다.
3단계: 어려움 및 가능한 접근 방식
우리가 평가해야 하는 표현식은 중첩된 극한과 적분을 포함하고 있어 직접 풀기가 매우 복잡합니다. 이 문제는 극한과 적분에 관련된 고급 미적분 개념을 이해하는지 테스트하기 위해 고안된 문제일 가능성이 높으며, 기본적인 방법으로 풀 수 있는 문제는 아닙니다.
4단계: 결론
고급 수학 도구가 없으면 질문에 대한 명확한 답변을 신뢰할 수 있게 제공할 수 없습니다. 문제의 복잡성은 기본적인 방법으로는 풀 수 없고, n → ∞로 갈 때 적분의 행동에 대한 통찰력을 제공하지만 완전한 해결책은 더 엄밀한 접근 방식을 요구한다는 것을 시사합니다.