나비에-스토크스 방정식
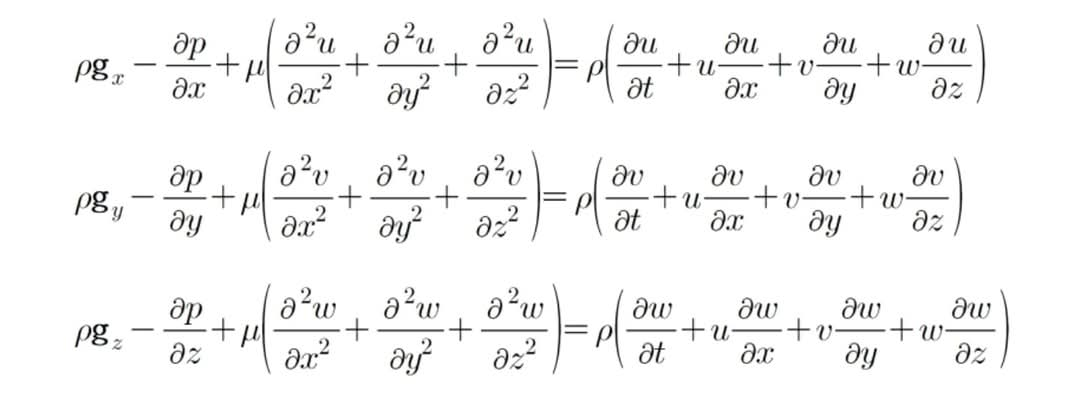



The image contains three Navier-Stokes equations in Cartesian coordinates. These equations describe the motion of viscous fluid substances. Let's analyze each equation:
Equation 1:
- Question: What is the x-component of the Navier-Stokes equation?
- Solution Process: The equation represents the conservation of momentum in the x-direction. The terms represent:
- \rho g_x: Body force in the x-direction (due to gravity).
- -\frac{\partial p}{\partial x}: Pressure gradient in the x-direction.
- \mu \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right): Viscous term representing the effect of viscosity on the fluid's motion in the x-direction. This is the Laplacian of the x-velocity component, u.
- \rho \left( \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} \right): Inertial term representing the acceleration of the fluid in the x-direction. This includes local acceleration (\frac{\partial u}{\partial t}) and convective acceleration (u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z}).
- Answer: The x-component of the Navier-Stokes equation is: \rho g_x - \frac{\partial p}{\partial x} + \mu \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right) = \rho \left( \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} \right)
- Key Concepts/Tips: The Navier-Stokes equations are a set of coupled, non-linear partial differential equations. Solving them analytically is often difficult, and numerical methods are frequently employed.
Equation 2:
- Question: What is the y-component of the Navier-Stokes equation?
- Solution Process: This equation is analogous to the x-component, but describes the conservation of momentum in the y-direction. The terms are similarly interpreted, with v representing the y-velocity component.
- Answer: The y-component of the Navier-Stokes equation is: \rho g_y - \frac{\partial p}{\partial y} + \mu \left( \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \frac{\partial^2 v}{\partial z^2} \right) = \rho \left( \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} \right)
- Key Concepts/Tips: The same key concepts and tips from Equation 1 apply here.
Equation 3:
- Question: What is the z-component of the Navier-Stokes equation?
- Solution Process: This equation describes the conservation of momentum in the z-direction, with w representing the z-velocity component.
- Answer: The z-component of the Navier-Stokes equation is: \rho g_z - \frac{\partial p}{\partial z} + \mu \left( \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} \right) = \rho \left( \frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z} \right)
- Key Concepts/Tips: The same key concepts and tips from Equation 1 apply here. These equations, along with the continuity equation, form a complete system for describing fluid flow.
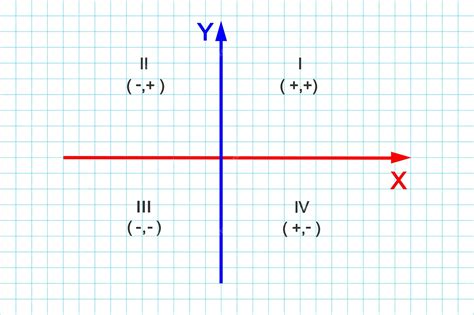
참고 : 카르테시안 좌표계
카르테시안 좌표계는 2차원 평면이나 3차원 공간에서 점의 위치를 나타내는 데 사용되는 좌표계입니다.
2차원 카르테시안 좌표계는 수직선 두 개를 서로 직교하도록 교차시켜 만들어집니다. 두 수직선의 교점을 원점이라고 하며, 각 수직선을 x축과 y축이라고 합니다. 평면 위의 점은 x축과 y축에 평행한 직선을 그어 두 축과 만나는 점의 좌표를 이용하여 나타냅니다.
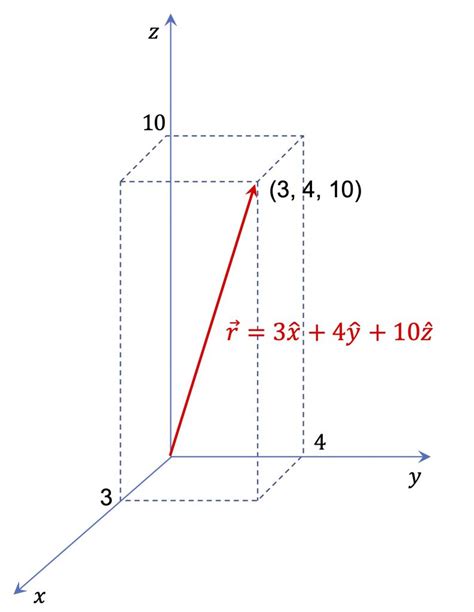
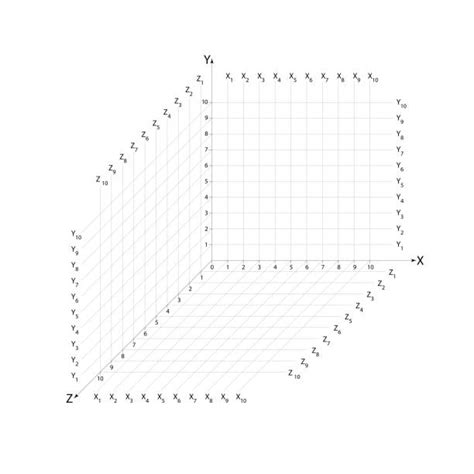
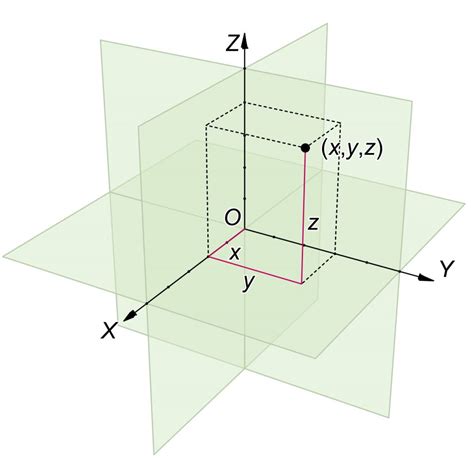
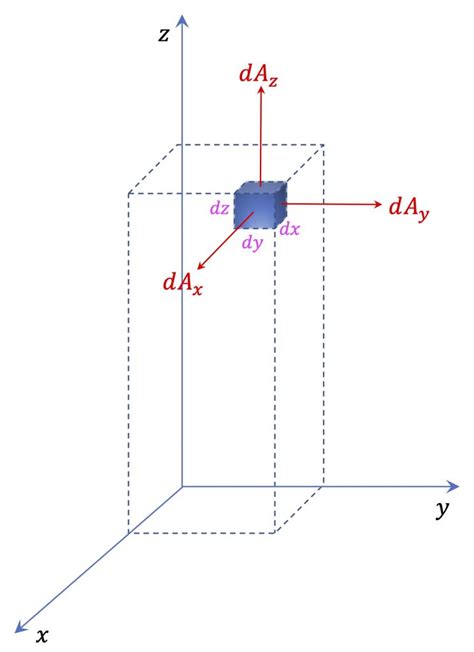
3차원 카르테시안 좌표계는 2차원 좌표계에 z축을 추가하여 만들어집니다. z축은 x축과 y축에 모두 직교하며, 원점을 지나는 수직선입니다. 공간상의 점은 x축, y축, z축에 평행한 직선을 그어 세 축과 만나는 점의 좌표를 이용하여 나타냅니다.
카르테시안 좌표계의 장점:
- 간단하고 직관적입니다.
- 점의 위치를 쉽게 표현할 수 있습니다.
- 기하학적 계산을 쉽게 수행할 수 있습니다.
카르테시안 좌표계의 단점:
- 곡선이나 곡면을 표현하기 어렵습니다.
- 극좌표계와 같은 다른 좌표계에 비해 특정 상황에서 불편할 수 있습니다.
예시:
- 2차원 평면에서 점 (2, 3)은 x축에서 2만큼, y축에서 3만큼 떨어진 위치에 있습니다.
- 3차원 공간에서 점 (1, 2, 3)은 x축에서 1만큼, y축에서 2만큼, z축에서 3만큼 떨어진 위치에 있습니다.
카르테시안 좌표계는 수학, 물리학, 공학 등 다양한 분야에서 널리 사용됩니다. 특히, 기하학적 계산, 그래프 작성, 벡터 표현 등에 유용하게 활용됩니다.