Discharge phenomenon of capacitor in RC circuit
아래 이미지는 RC 회로에서 커패시터의 방전을 모델링하는 방법을 설명하고 있습니다. 스페인어로 작성되었으며, 수식과 그림을 함께 사용하여 다음 내용을 설명합니다.
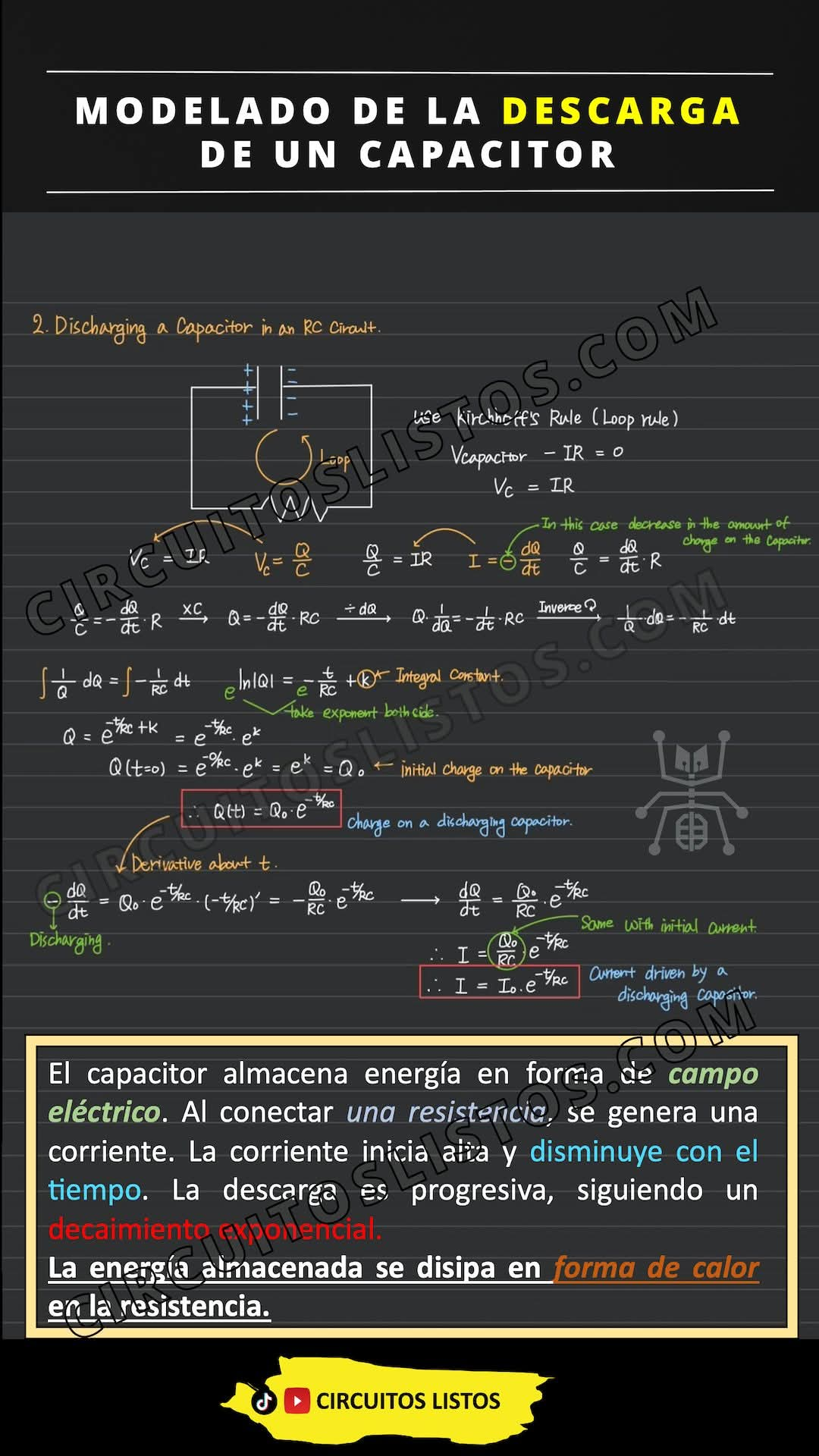
1. 키르히호프 전압 법칙의 적용: 폐회로에서 커패시터의 전압과 저항의 전압 관계를 키르히호프 전압 법칙을 이용하여 나타냅니다.
2. 미분 방정식 유도 및 해석: 전류를 전하량의 시간에 대한 미분으로 정의하고, 이를 이용하여 1차 선형 동차 미분 방정식을 유도합니다. 이 방정식의 해는 지수 함수 형태이며, 시간에 따른 전하량의 감소를 나타냅니다. RC 시간 상수가 이 감소 속도를 결정합니다.
3. 방전 과정 설명: 커패시터는 전기장의 형태로 에너지를 저장합니다. 저항을 연결하면 전류가 흐르고, 전류는 처음에는 크지만 시간이 지남에 따라 감소합니다. 이 방전 과정은 지수 함수적 감소를 따르며, 저장된 에너지는 저항에서 열로 소산됩니다.
요약: 이미지는 수학적 모델링을 통해 RC 회로에서 커패시터의 방전 현상을 설명하고, 전하량과 전류의 시간에 따른 변화를 지수 함수로 표현하고 있습니다. 전기 회로 이론과 미분 방정식에 대한 기본적인 이해가 필요합니다.
커패시터 방전 (자세한 설명) ✅
커패시터 ⚡️가 저항을 통해 방전되는 과정은 키르히호프 전압 법칙을 적용하여 모델링됩니다. 이 법칙은 폐회로에서 커패시터 전압과 저항 전압 사이의 관계를 설명합니다 🕵️♂️.
방전 모델링을 위해 전류를 전하량의 시간에 대한 미분으로 정의합니다. 이는 1차 선형 동차 미분 방정식을 도출하여 시간에 따른 전하량 변화를 설명합니다 ⌚️.
이 방정식을 풀면 지수 함수 형태의 해를 얻게 되는데, 이는 RC 시간 상수에 의해 제어되는 전하량의 점진적인 감소를 나타냅니다. RC 시간 상수는 저항과 커패시턴스의 곱으로 정의됩니다.
위의 이미지에 기술된 미분 방정식 유도 과정을 재현해보면 다음과 같다.
1. 키르히호프 전압 법칙 적용:
폐회로에서 키르히호프 전압 법칙을 적용하면 다음과 같은 식이 성립합니다.
V<sub>c</sub> - IR = 0
여기서:
- V<sub>c</sub> 는 커패시터의 전압
- I 는 회로의 전류
- R 은 저항의 저항값
2. 커패시터 전압과 전하량의 관계:
커패시터의 전압과 전하량( Q ) 사이에는 다음과 같은 관계가 있습니다.
V<sub>c</sub> = Q/C
여기서 C 는 커패시터의 정전용량입니다.
3. 전류와 전하량의 관계:
전류는 단위 시간당 흐르는 전하량의 변화율이므로 다음과 같이 표현할 수 있습니다.
I = dQ/dt
4. 미분 방정식 유도:
위의 세 가지 식을 조합하면 다음과 같은 미분 방정식을 얻을 수 있습니다.
Q/C - R(dQ/dt) = 0
이 식을 정리하면 다음과 같은 1차 선형 동차 미분 방정식을 얻습니다.
dQ/dt + (1/RC)Q = 0
이 미분 방정식을 풀면 커패시터의 전하량이 시간에 따라 어떻게 변하는지를 알 수 있습니다. 이미지에서는 이 미분 방정식을 풀어 Q(t) = Q₀e^(-t/RC) 와 같은 해를 얻는 과정을 보여줍니다. 여기서 Q₀ 는 초기 전하량입니다.
#전자공학 #전기공학 #물리학