프레네-세레 공식 (Frenet-Serret formulas)
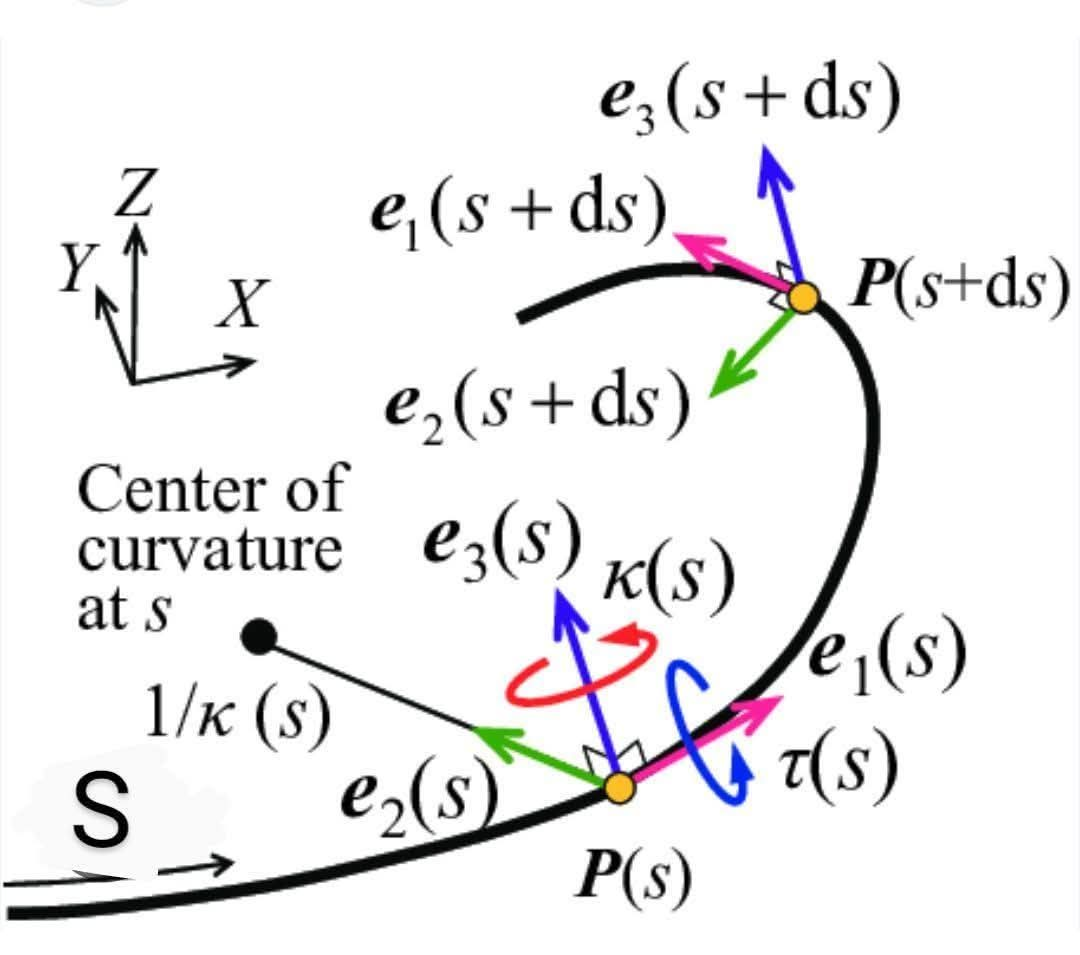
이 이미지는 곡선의 **프레네-세레 공식 (Frenet-Serret formulas)**을 설명하기 위한 도식입니다. 구체적으로는 곡선 상의 한 점에서의 접선 벡터, 법선 벡터, 그리고 접선 벡터와 법선 벡터가 미소 변위 ds 만큼 이동했을 때의 변화를 보여줍니다.
핵심 내용:
- 곡선: 두께가 없는 매끄러운 곡선이 표현되어 있습니다. s 는 곡선의 아크 길이(arc length)를 나타내는 매개변수입니다. P(s) 는 곡선 상의 점을 나타냅니다.
- 좌표계: 데카르트 좌표계 (X, Y, Z)가 표시되어 있으며, 이를 기준으로 곡선의 기하학적 특성을 분석합니다.
- 프레네 틀 (Frenet frame): 곡선 상의 점 P(s) 에서 접선 벡터 e₁(s) , 법선 벡터 e₂(s) , 그리고 곡률 벡터 e₃(s) 로 이루어진 국소 좌표계 (프레네 틀)가 표현되어 있습니다. 이 벡터들은 서로 직교합니다.
- 곡률 (Curvature): κ(s) 는 곡선의 곡률을 나타냅니다. 곡률은 곡선이 얼마나 휘어져 있는지를 나타내는 척도이며, 곡률 반지름 1/κ(s) 은 곡률 중심까지의 거리를 나타냅니다.
- 토션 (Torsion): τ(s) 는 곡선의 토션(비틀림)을 나타냅니다. 토션은 곡선이 공간에서 어떻게 비틀리는지를 나타내는 척도입니다.
- 미소 변위: ds 만큼 곡선을 따라 이동했을 때, 프레네 틀의 벡터들이 어떻게 변하는지를 보여줍니다. 이 변화는 곡률과 토션에 의해 결정됩니다. P(s+ds) 는 ds 만큼 이동한 후의 점을 나타냅니다.
프레네-세레 공식과의 연관성:
이 이미지는 프레네-세레 공식을 직관적으로 이해하는 데 도움을 주는 시각적 자료입니다. 프레네-세레 공식은 접선 벡터, 법선 벡터, 곡률 벡터의 미분을 곡률과 토션으로 표현하는 미분 방정식입니다. 이미지에서 보이는 벡터들의 변화는 바로 이 공식을 시각적으로 나타낸 것입니다. 수식으로는 다음과 같이 표현됩니다 (단, ' 는 s 에 대한 미분을 나타냅니다):
- e₁' = κe₂
- e₂' = -κe₁ + τe₃
- e₃' = -τe₂
결론: 이 이미지는 미적분학과 벡터 해석학의 지식을 바탕으로 이해해야 합니다. 곡선의 기하학적 성질을 연구하는 데 중요한 개념인 프레네-세레 공식을 시각적으로 설명하는 데 효과적입니다.
Frenet-Serret formulas
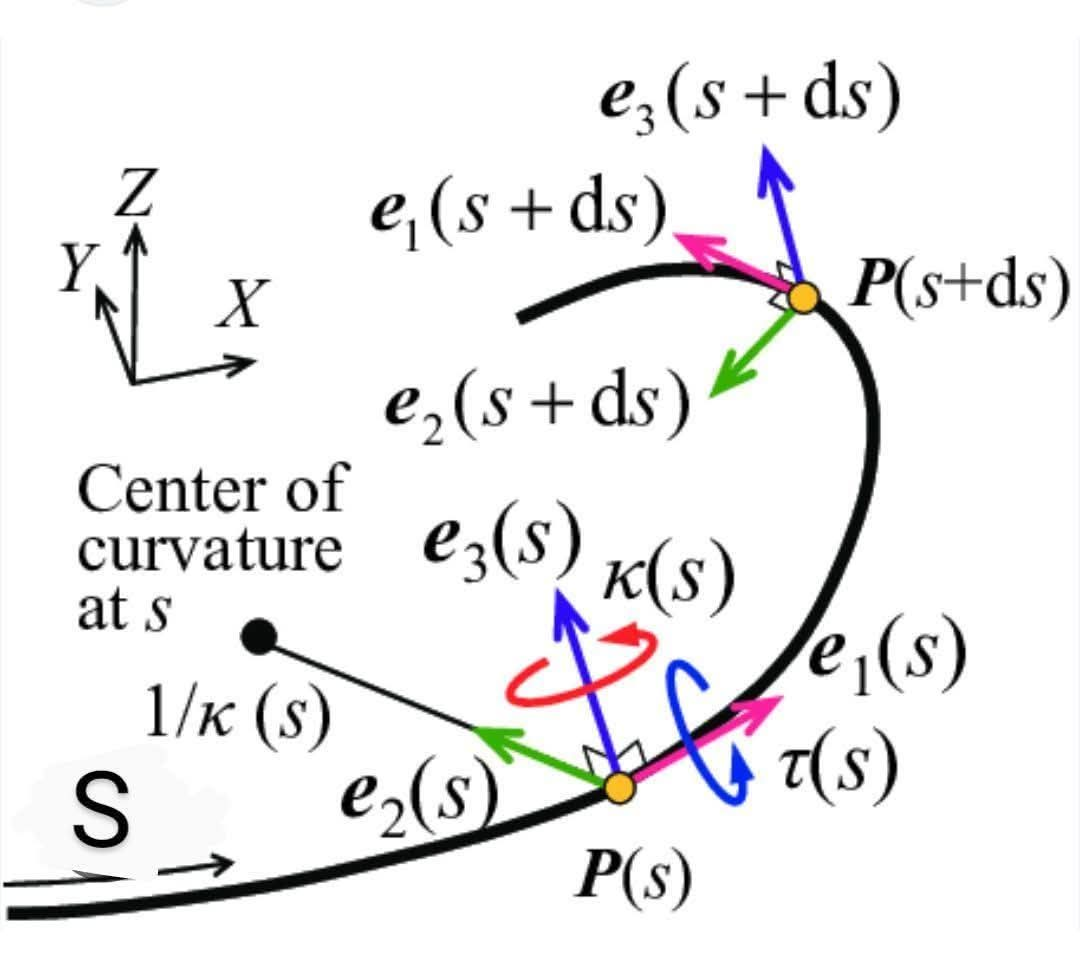
This image is a diagram to illustrate the Frenet-Serret formulas of a curve. Specifically, it shows the tangent vector, normal vector, and curvature vector at a point on the curve, as well as how these vectors change when they move by a small displacement ds .
Key Points:
- Curve: A smooth curve without thickness is represented. s is the parameter representing the arc length of the curve. P(s) represents a point on the curve.
- Coordinate System: A Cartesian coordinate system (X, Y, Z) is shown, and the geometric properties of the curve are analyzed based on this system.
- Frenet Frame: The local coordinate system (Frenet frame) consisting of the tangent vector e₁(s) , the normal vector e₂(s) , and the curvature vector e₃(s) at the point P(s) on the curve is represented. These vectors are orthogonal to each other.
- Curvature: κ(s) represents the curvature of the curve. Curvature is a measure of how much a curve bends, and the radius of curvature 1/κ(s) represents the distance to the center of curvature.
- Torsion: τ(s) represents the torsion (twist) of the curve. Torsion is a measure of how a curve twists in space.
- Small Displacement: The image shows how the vectors of the Frenet frame change when moving along the curve by ds . This change is determined by the curvature and torsion. P(s+ds) represents the point after moving by ds .
Relationship to Frenet-Serret Formulas:
This image is a visual aid for intuitively understanding the Frenet-Serret formulas. The Frenet-Serret formulas are differential equations that express the derivatives of the tangent vector, normal vector, and curvature vector in terms of curvature and torsion. The changes in the vectors shown in the image are a visual representation of these formulas. Mathematically, they can be expressed as follows (where ' denotes differentiation with respect to s ):
- e₁' = κe₂
- e₂' = -κe₁ + τe₃
- e₃' = -τe₂
Conclusion: This image requires knowledge of calculus and vector analysis to understand. It is effective in visually explaining the Frenet-Serret formulas, which are important concepts in studying the geometric properties of curves.