new geometric radius
기하학적 정체성의 새로운 리더십 아래에 있는 라디안에 대한 서론:
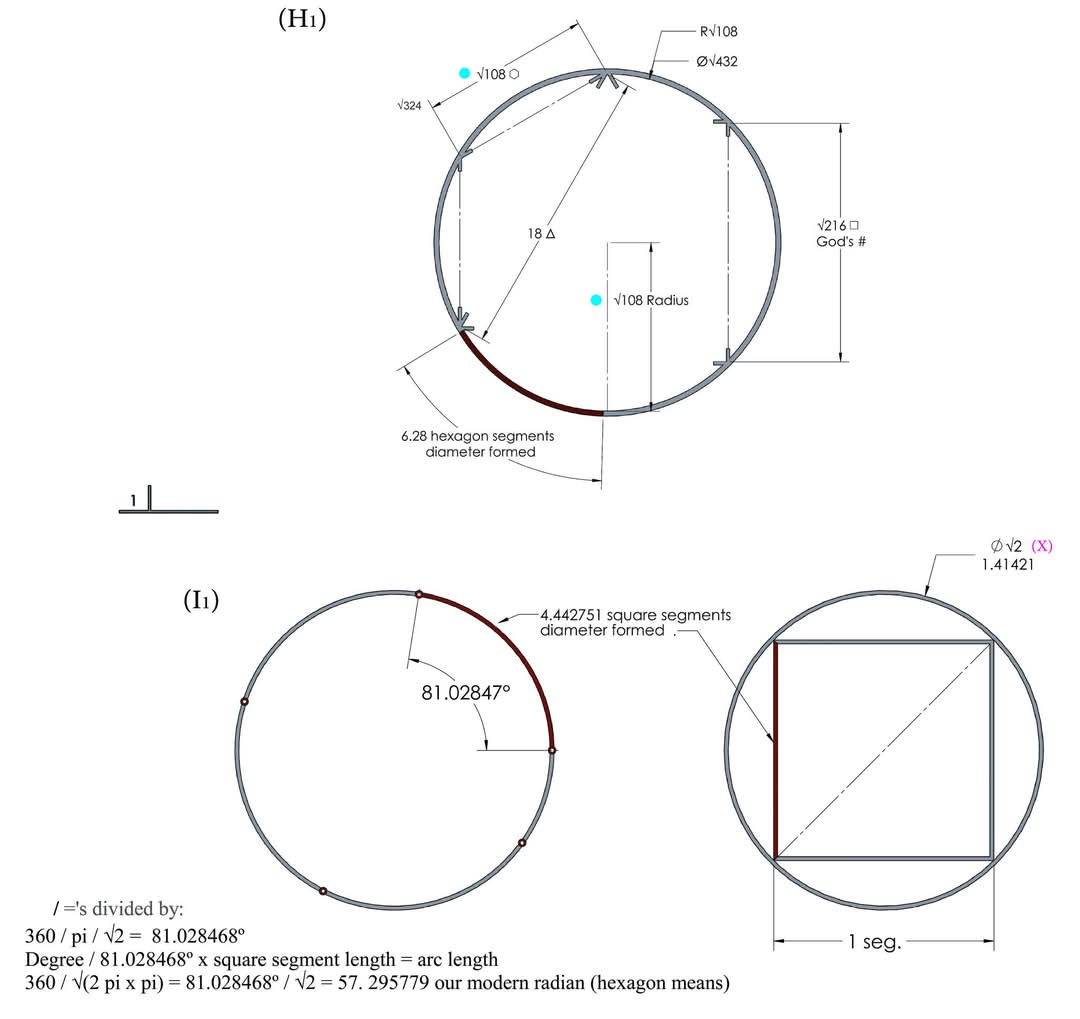
제1일러스트레이션
우선, 부모 다각형의 지도하에 있는 형제 라디안은 다각형 각도 측정의 자체 큐빗을 가지고 있으며, #-곤이 많을수록 각 다각형에 대한 큐빗 반경 특이적이며 모두 서로의 세대 비율 내에 있다. 직경의 반경과 육각형 세그먼트의 길이는 동일하다(H1).
로버트 코테스와 현대 과학은 잘못된 라디안 세그먼트 전제를 적용한다. 반지름이 아니라 자 척도 식별의 삼각법과 물리학에 적분되는 것은 육각형 세그먼트 의미이다. 플라톤의 플라톤 입체체의 처음 두 면, 정육면체의 정사각형 면과 정사면체의 정삼각형 면의 구성에서 다음과 같은 방사형은 인식을 향상시킬 것이다. 4곤 정사각형 단위 원(I1), 하나의 정사각형 세그먼트가 81.028도에서 단위 둘레를 감았을 때 만들어지는 각도.
스키 리더를 위해
수학이 당신의 것이 아니라면, ♦ 교훈은 다음과 같다. 라디안은 독점적으로 다각형 수단이다; 원 형태의 선형 측정은 도 사이의 반경 측정의 특이점에 있다. 즉, 선형 및 방사형 큐빗 측정은 특이점이다.
제2차 삽화
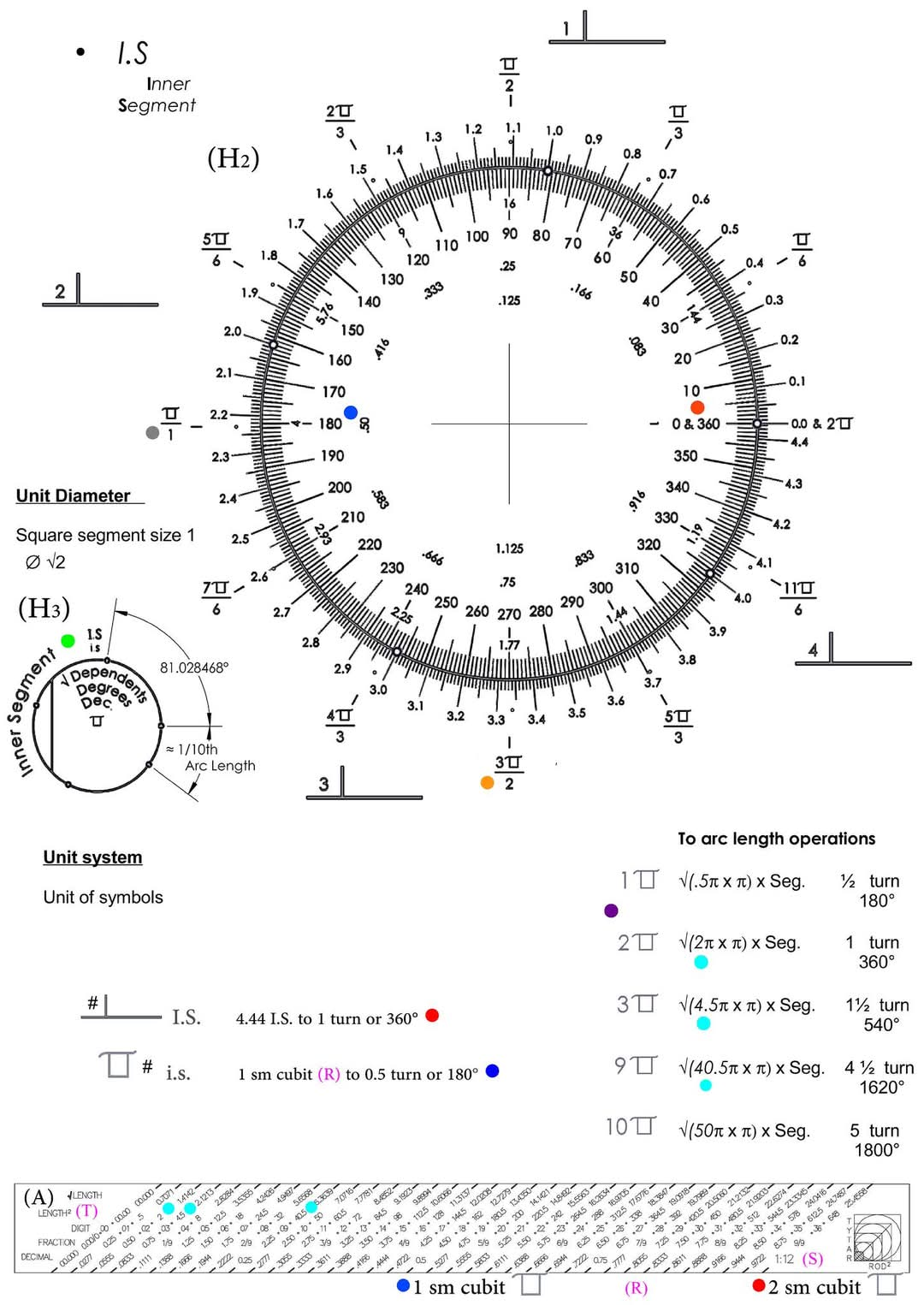
예시된 바와 같은 더 작은 직경(H3)은 동일한 정사각형 세그먼트 아래에서 기하학의 새로운 리더십 하에 재정의된 라디안이며, 이는 √2 종동 디지트(X에서 W)를 생성한다는 것을 의미한다. 즉, 아크 길이를 결정하기 위해 현대 반경 세그먼트가 사용되는 대신, 원주형으로 형성된 정사각형 세그먼트가 아크 길이 통신으로 사용된다. ♦ 정사각형의 √2 대각선 수단도 외접 수단이기 때문에, 큐빗 엔지니어링 스케일 측정 내의 정사각형 교정 무기고가 생성된다. 또한 고대인들은 선형 직각과 원형 정도 탐색을 위해 갈대와 매듭이 있는 밧줄을 사용했으며, 다음은 이러한 유사성 시스템을 표시하는 데 대한 액세스이다. 더 명확한 자 눈금 해상도가 필요한 경우 다음 그림을 스크롤하십시오.
그림 (H3)에 표시된 것은 이 큐빗의 방사형 평균에 대해 제시된 정사각형 다각형 세그먼트인 √2 단위 원의 유리 학년이다. 이 정사각형 단위 원의 둘레 길이는 (H2)에 표시된 원과 같이 둘레 길이로 형성된 4.4428개의 내부 정사각형 세그먼트 직경의 합인 √(2pi x pi)의 측정과 수치적으로 동일하다. (H2)에도 나와 있듯이, 36자리에 10을 곱한 원으로 형성된 직경을 감싸는 1" 단위 자 눈금(A at R)의 2개의 작은 큐비트를 회전/회전 단위(S)의 하나의 큐비트 자 눈금(A)인 반경 방향 측정 360o로 눈금을 ♦. 여기서 하나의 작은 큐빗은 자 눈금에서 18번째 자리와 같고 ●(파란색 점)에 10을 곱하면 직경에서 180o 배치와 같다. 2개의 작은 큐빗은 자 눈금에서 36자리와 같고●(빨간 점)에 10을 곱하면 직경에서 360o 배치와 같다. ♦ 즉, 전자의 2파이 라디안 방법은 한 회전에서 2개의 작은 큐빗이 되었고 모든 큐빗 자 눈금(A) 선형 측정은 현재 방사형으로 방송된다. 1 큐비트 ●(파란색 점)은 180o 또는 180o 나누기 10, 즉 숫자 자 눈금에서 18번째 자리 위치, 본질적으로 반 자 눈금 및/또는 회전에 있다. 존중하여, 3 큐비트는 54자리 또는 540o에서 자 눈금과 반 또는 반 또는 회전과 같을 것이다.
더 큰 직경(H2)의 바닥에 위치하는 270o 분율 3/2●(주황색 점)을 예측하기 위해, 3에 180을 곱한 것은 540o/2는 270o를 분수 분모 2●(주황색 점)로 나눈 것이다. ♦도를 10으로 나눈 것은 선형 큐빗 자 눈금 관리에서의 자릿수 배치당 회전과 같다. 삽화의 맨 오른쪽 중간에는 열에 번호가 매겨진 기호●(보라색 점)이 있다. 이것들은 더 큰 직경 주위에 표시되는 회전의 큐빗 및 분수 배치입니다. 기호 pi는 반지름에서 pi 라디안까지 연관되어 있습니다. 따라서 나는 정사각형 선분을 ●(자두점)의 방사형 수단과 구별하기 위해 새로운 기호를 만들었다. "새로운 기호"가 있는 열의 숫자는 작은 큐빗 방사형 평균(R)에 해당한다.
방정식과 방사형 수가 자 척도에 통합되는 곳은 이제 제곱 기하학적 틀이다. 더 자세히 설명하자면, ●(보라색 점)의 첨부 열에서 2 새로운 기호 큐빗은 2 x pi x pi의 근을 곱한 내부 일치 정사각형 세그먼트 ●(녹색 점)와 동일하며, 합 4.4428 정사각형 세그먼트 원은 한 회전에서 단위 직경의 원주 길이와 동일한 길이를 형성한다. 따라서, 3 세제곱에서의 다음 공식, 정사각형 세그먼트 길이에 4.5 x pi x pi의 근을 곱한 것, 합은 6.6643이고 ●(회색 점)의 분수 분모 1로 나눈 1.5회전에서의 호 길이이다. ♦ 전자 2pi 라디안을 2 세제곱 반경 측정으로 교환함으로써 선형 세제곱/자리 자 눈금 계층이 반경 및 선형 측정의 무기고로 사용될 수 있음을 주목한다.
√# pi x pi 번호 자체의 항등식은 막대(T)의 √길이 제곱 티어에서 숫자 막대(A)에 의해 생성되었다. ●(테알 도트) 주; (A) 행의 숫자 2에 위치한 ●(테알 도트)의 ●의 파이 '호 길이 연산' 방정식의 번호에서, 새로운 기호 #파이 x 파이 연산 ●(보라색 도트)에서 첫 번째 숫자를 표시한다. 자릿수 3(T)에 위치하는 4.5의 제곱근●(teal dot)은 자릿수 9, 40.5 등에 위치한다. ♦ 즉, 자릿수와 할당된 √길이 제곱 티어(T)는 ●(자색 점)에서 √(# pi x pi) 연산들의 주요 큐빗 회전 소스 중 하나이다.
제3 삽화
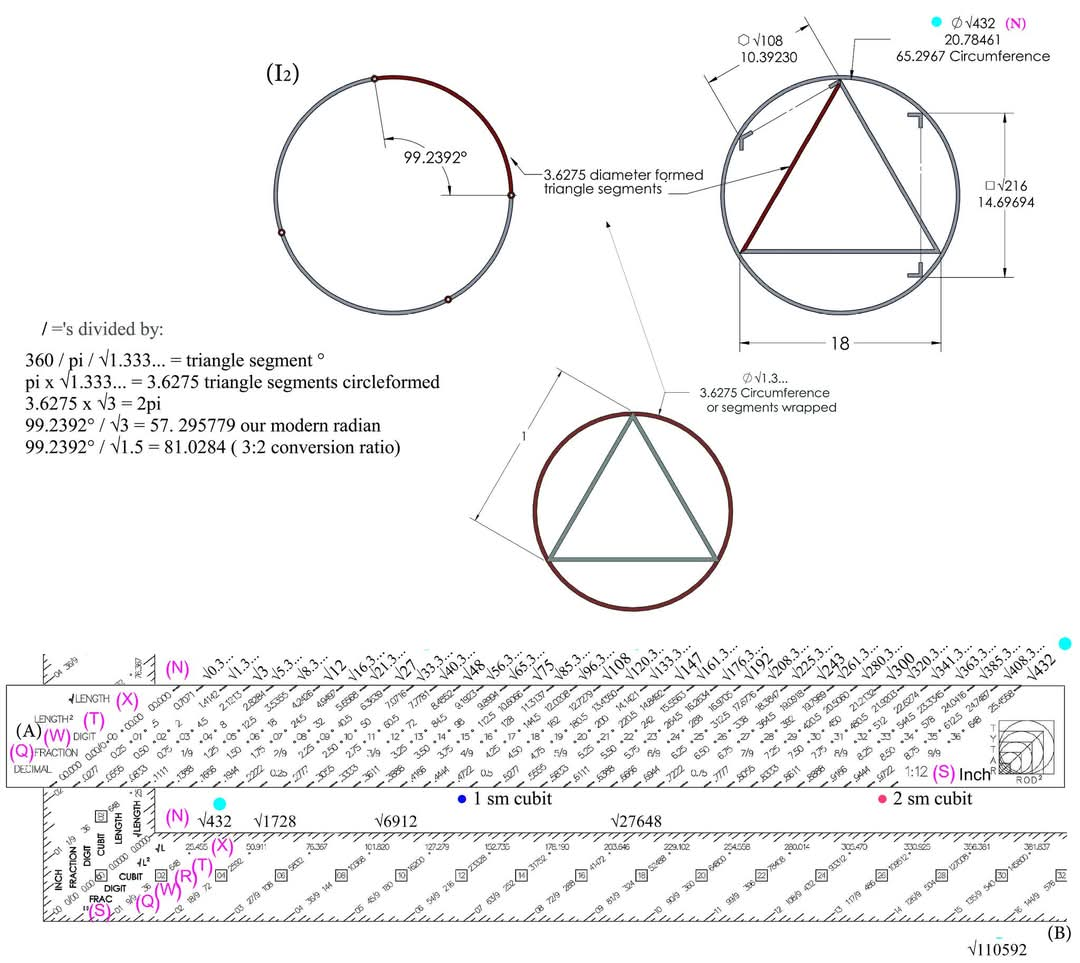
다각형과 플라톤 고체를 방사형 관점에 넣기 위해 (I2) 직경을 감싸고 있는 3-곤 세그먼트는 방사형 항행의 완전히 새로운 리더십 하에 삼각형 세그먼트를 형성한 3.6275원과 같다. 이것은 √3 티어(N에서의 A)에 대한 반경 방향 수단이 될 것이다. √(1.3...pi x pi)의 새로운 방사형 응용 프로그램이 이제 √3 계층()에서 배치된다. 단위 √(2pi x pi)와 동일한 방식으로 자릿수(A) 스케일의 N)은 이전에 (X)에서 전개되었다. ♦ 6-곤(육각형), 4-곤(제곱) 및 3-곤(삼각형)에서 보여지는 것처럼 반경은 다각형 세그먼트의 원주 평균에 대한 자연스러운 과정이지 오늘날의 반경 평균이 아니다. 예시 전체에 사용된 다각형은 현대 권위를 넘어 인식을 옮기는 것이었습니다.