황금비율


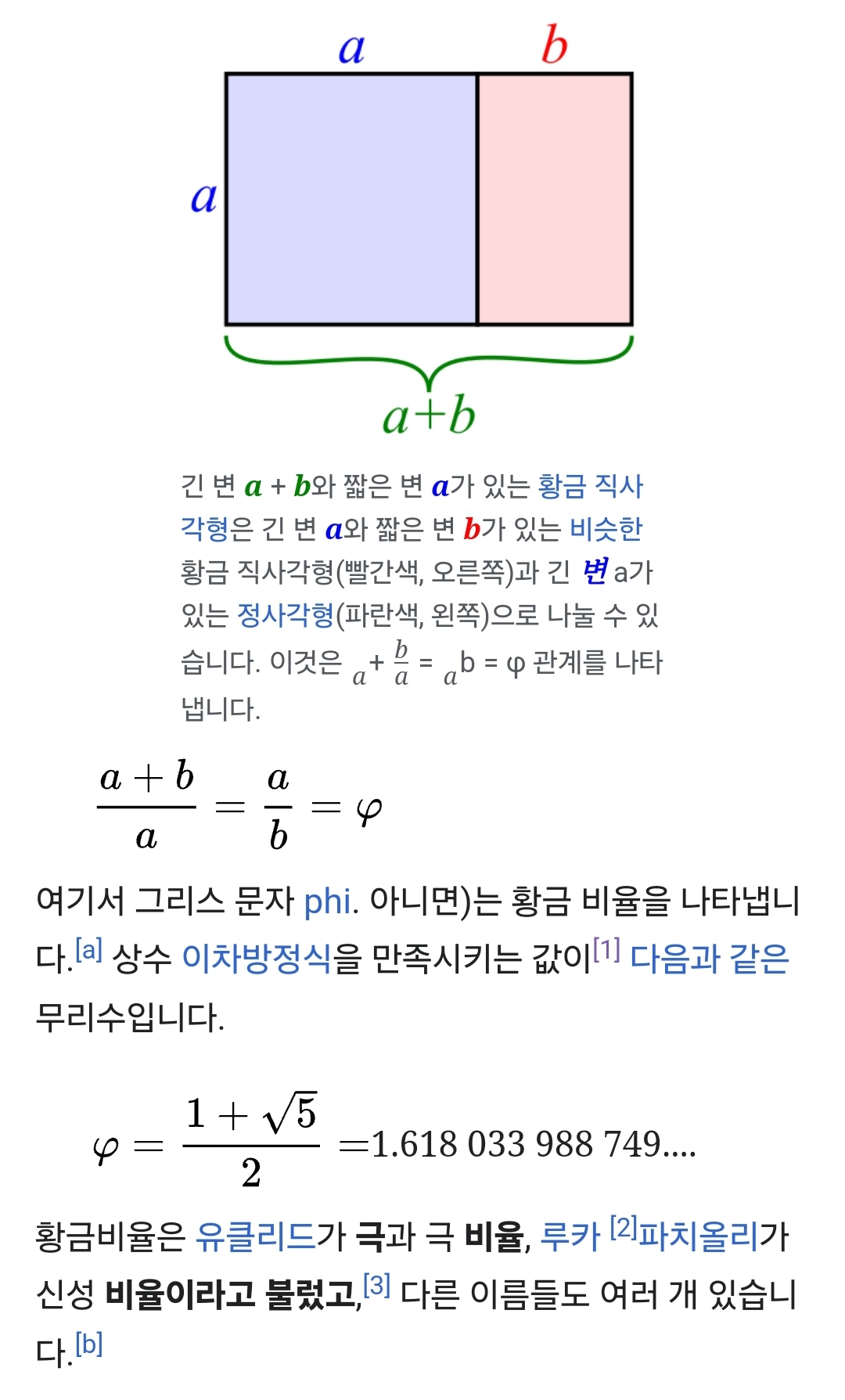
수학자들은 고대부터 황금비의 성질을 연구해 왔습니다. 이것은 정 오각형의 대각선과 그 변의 비율이고 따라서 정십이면체와 정십이면체의 구성에 나타납니다.[7] 황금색 직사각형, 즉 가로 세로 비율이 다음과 같은 직사각형{\displaystyle \varphi}— 가로 세로 비율이 같은 정사각형과 작은 직사각형으로 자를 수 있습니다. 황금 비율은 데이터에 대한 불확실한 적합성을 기반으로 금융 시장과 같은 자연물 및 인공 시스템의 비율을 분석하는 데 사용되었습니다.[8] 황금 비율은 잎과 식물의 다른 부분의 나선형 배열을 포함하여 자연의 일부 패턴에서 나타납니다.
르 코르뷔지에와 살바도르 달리를 포함한 일부 20세기 예술가와 건축가들은 그들의 작품이 대략적인 황금 비율에 비례한다고 믿었습니다. 이러한 용도는 종종 황금 직사각형 형태로 나타납니다.
계산

역사
참고 항목: 수학과 예술 그리고 피보나치 수 §의 역사
마리오 리비오에 의하면
고대 그리스의 피타고라스와 유클리드부터 중세 이탈리아 수학자 피사의 레오나르도, 르네상스 천문학자 요하네스 케플러에 이르기까지 옥스포드 물리학자 로저 펜로즈와 같은 오늘날의 과학자들까지 모든 시대의 가장 위대한 수학자들 중 일부는 이 단순한 비율과 그 속성을 놓고 끝없는 시간을 보냈습니다... 생물학자, 예술가, 음악가, 역사가, 건축가, 심리학자, 심지어 신비주의자들도 그것의 보편성과 매력의 근거에 대해 곰곰이 생각하고 토론했습니다. 사실, 황금비율은 수학 역사상 다른 어떤 숫자도 아닌 모든 학문의 사상가들에게 영감을 주었다고 말할 수 있습니다.[11]
— The Golden Ratio: The Story of Phi, the World's Most Astonishing Number
고대 그리스 수학자들은 금빛 비율이 기하학에 자주 등장하기 때문에 처음으로 연구했습니다;[12] 한 선을 "극한 비율과 평균 비율"로 나누는 것은 규칙적인 오각형과 오각형의 기하학에서 중요합니다.[13] 기원전 5세기 수학자 히파수스는 황금비가 정수도 분수도 아니라는 사실을 밝혀내 피타고라스 사람들을 놀라게 했다고 합니다.[14] Euclid's Elements (기원전 300년경)는 황금비를 사용하는 몇 가지 명제와 그 증명을 제공하며,[15][c] 다음과 같이 진행되는 최초의 알려진 정의를 포함합니다.[16]
직선은 전체 선이 더 큰 세그먼트에 있을 때 극단적이고 평균적인 비율로 절단되었다고 합니다. 그리고 더 큰 세그먼트에 있을 때 더 작은 세그먼트에 대해서도 마찬가지입니다.[17][d]

황금 비율은 다음 천년에 걸쳐 주변적으로 연구되었습니다. 아부 카밀 (850–930년경)은 오각형과 십각형의 기하학적 계산에 그것을 사용했습니다; 그의 글은 관련 기하학 문제에서 비율을 사용했지만 그것이 피보나치 수와 연결되어 있다는 것을 관찰하지 못한 피보나치 (1170–1250년경)의 글에 영향을 미쳤습니다.[19]
루카 파치올리(Luca Pacioli)는 그의 책을 비율을 따서 디비나 비례라고 이름 지었습니다; 피에로 델라 프란체스카(Piero della Francesca)의 대부분을 표절한 이 책은 플라톤 고체의 일부에 나타나는 것을 포함하여 그 속성을 탐구했습니다.[20][21] Pacioli의 책을 설명한 Leonardo da Vinci는 이 비율을 aurea ('황금 섹션')[22]이라고 불렀습니다. 흔히 파치올리가 즐겁고 조화로운 비율을 산출하기 위한 황금 비율의 적용을 옹호했다고 하지만, 리비오는 이 해석이 1799년의 오류로 추적되고 있으며, 파치올리가 실제로 유리 비율의 비트루비우스 체계를 옹호했다고 지적합니다.[23] 파치올리는 또한 그 비율에서 가톨릭의 종교적 중요성을 보았고, 이것이 그의 작품의 제목으로 이어졌습니다. 라파엘 봄벨리와 같은 16세기 수학자들은 이 비율을 사용하여 기하 문제를 풀었습니다.[24]
독일 수학자 시몬 야코프(Simon Jacob, 1564년경)는 연속적인 피보나치 수들이 황금 비율로 수렴한다는 것에 주목했습니다;[25] 이것은 1608년 요하네스 케플러에 의해 재발견되었습니다.[26] (역)황금비의 첫 번째 알려진 십진법 근사치는 "약"으로 표시되었습니다.{\displaystyle 0.6180340}{\displaystyle 0.6180340}" 1597년 튀빙겐 대학교의 미하엘 마에슬린이 케플러에게 보낸 편지.[27] 같은 해, 케플러는 황금비와 피타고라스 정리를 결합한 케플러 삼각형의 마에슬린에게 편지를 썼습니다. 케플러는 다음과 같이 말했습니다.
기하학에는 두 가지 위대한 보물이 있습니다: 하나는 피타고라스의 정리이고, 다른 하나는 한 선을 극한과 평균 비율로 나누는 것입니다. 첫 번째는 금 덩어리에 비유할 수 있고, 두 번째는 귀중한 보석이라고 부를 수 있습니다.[28]
18세기 수학자 아브라함 드 모이브르, 니콜라오스 1세 베르누이, 레온하르트 오일러는 피보나치 수열의 위치를 기반으로 하여 피보나치 수열의 값을 구하는 황금비 기반 공식을 사용했습니다. 1843년 자크 필리프 마리 비네에 의해 재발견되었고, 그 때문에 비네 공식으로 명명되었습니다.[29] 마르틴 옴은 1835년에 독일어로 황금률을 설명하기 위해 슈니트('황금 구간')라는 용어를 처음 사용했습니다.[30] James Sully는 1875년에 그에 상응하는 영어 용어를 사용했습니다.[31]
1910년까지 발명가 Mark Barr는 그리스 문자 phi를 사용하기 시작했습니다.{\displaystyle \varphi})[32][e]는 황금 비율을 나타내는 기호입니다. 타우(tau)로 표현되기도 했습니다.{\displaystyle \tau }{\displaystyle \tau })는 고대 그리스어 το μ ή의 첫 글자('컷' 또는 '섹션')입니다.

1960년대 후반 스티브 베어가 개발한 줌 구성 체계는 정이십면체/십면체의 대칭 체계를 기반으로 하며, 황금 비율을 편재적으로 사용합니다. 1973년과 1974년 사이에 로저 펜로즈는 두 마름모 타일의 면적 비율과 패턴 내 상대적 빈도 모두에서 황금 비율과 관련된 패턴인 펜로즈 타일을 개발했습니다.[36] 이는 1982년 댄 셰흐트만이 20면체 대칭을 갖는 준결정을 노벨상으로 발견한 후 관심을 끌었고, 이는 곧 펜로즈 타일과의 유사성을 통해 설명되었습니다.[37]
수학(Mathematics)
비합리성



최소다항식 : Minimum polynomial
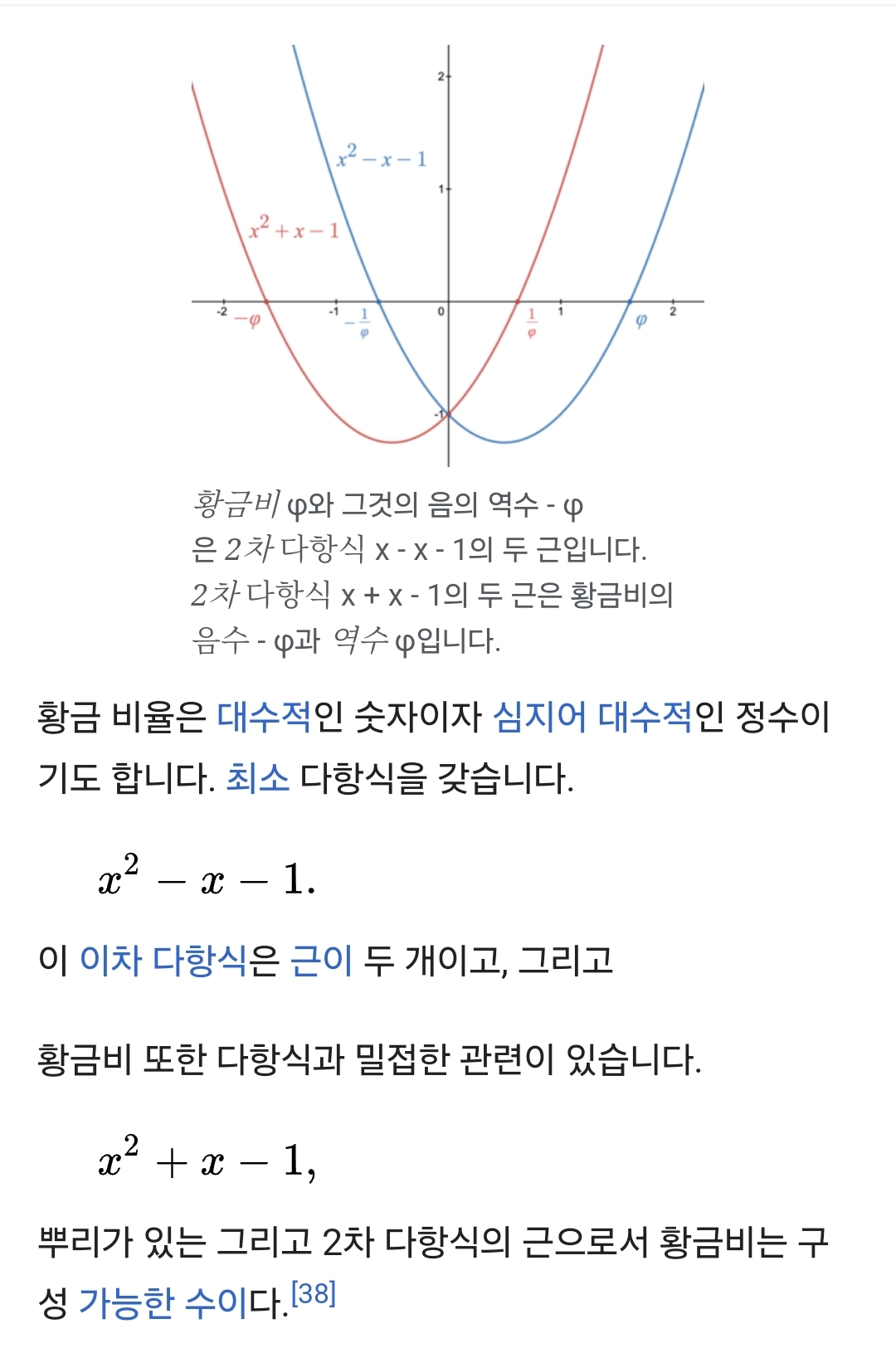
황금비율 공액과 거듭제곱 : Golden ratio Gongsu and power